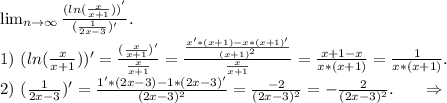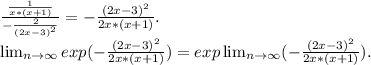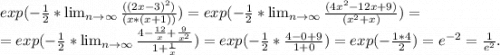Ответы на вопрос:
Відповідь:
1) Оскільки піраміда має 1001 грань, то її основа має 1000 сторін.
2) Піраміда має 2002 ребра.
Покрокове пояснення:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Сначала цена костюма возросла на 5%,а потом снизилась на 20% .после...
 gaglovev200131.03.2022 08:10
gaglovev200131.03.2022 08:10 -
Решите уравнение: а) 7а = –41,6 + 3а; 2. в одной клетке в 4 раза...
 ilyashamonin14.09.2022 14:52
ilyashamonin14.09.2022 14:52 -
1) на двух участках посадили одиковыми кусты смородины. на 1 участке...
 Eka22814.11.2021 14:42
Eka22814.11.2021 14:42 -
Пеппиотправиласьзапокупками в соседний город . ейнадопроехать 39...
 aimsen18.12.2022 08:12
aimsen18.12.2022 08:12 -
Цена товара в первый месяц возросла на 20%, а во второй раз ещё...
 minskaya8624.06.2020 15:42
minskaya8624.06.2020 15:42 -
Кзавтрашнему на берегу озера байкал, город - герой, находящийся...
 RusskikhDaria24.06.2022 12:04
RusskikhDaria24.06.2022 12:04 -
Маша и миша задумали одинаковые числа. если число маши увеличить...
 wartander59522.07.2020 06:33
wartander59522.07.2020 06:33 -
Решите уравнение: а)(х-3.25)*3.6=1.62; б)5.9у+2.3у=27.88 !...
 Anton22266622202.06.2023 15:34
Anton22266622202.06.2023 15:34 -
Хозяйство закупило саженцы яблонь по 15 000р. и саженцы груш по...
 snezhanakosola13.02.2021 17:04
snezhanakosola13.02.2021 17:04 -
Отодной пристани в разных направлениях отошли две моторные локи.скорость...
 nikitka101113.06.2022 19:05
nikitka101113.06.2022 19:05

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

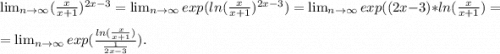 Применяем первое правило Лопиталя:
Применяем первое правило Лопиталя: