Регистрация Спросить otvet5GPT
Kostyaofficial
07.07.2022 12:06
Алгебра
Есть ответ 👍

Сумма первых трёх чисел возрастающей геометрической прогрессии равна 65. Если к этим числам прибавить 33,27, 1 соответственно, то получится арифметическая прогрессия. Найдите пятый член исходной геометрической прогрессии.

251
353
Посмотреть ответы 2

Ответы на вопрос:

krivobokova45
krivobokova45
4,7(69 оценок)

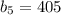
ответ: b_5=405

Объяснение:

В геометрической прогрессии с первым членом b₁ и знаменателем q

Так как прогрессия возрастающая то q> 1 ; b₁>0

Cумму первых трех членов можно представить в виде :

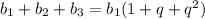
b_1+b_2+b_3=b_1(1+q+q^2)

По условию :

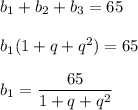
b_1+b_2+b_3=65 b_1(1+q+q^2)=65 b_1=\dfrac{65}{1+q+q^2}

Также сказано что

Если к этим числам прибавить 33,27, 1 выйдет арифметическая прогрессия

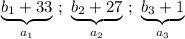
\underbrace{b_1+33}_{a_1} \ ; \ \underbrace{b_2+27}_{a_2} \ ; \ \underbrace{b_3+1}_{a_3}

Тогда будет верно равенство

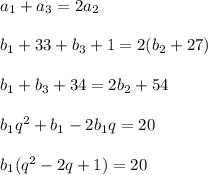
a_1+a_3=2a_2 b_1+33+b_3+1=2(b_2+27) b_1+b_3+34=2b_2+54 b_1q^2+b_1-2b_1q=20 b_1(q^2-2q+1)=20

Подставим

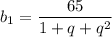
b_1=\dfrac{65}{1+q+q^2}

Выйдет :

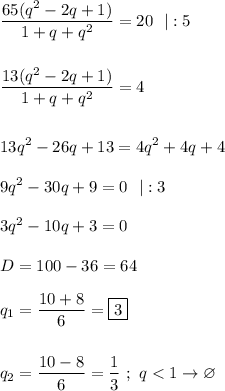
\displaystyle \frac{65(q^2-2q+1)}{1+q+q^2} =20 \ \ |:5 frac{13(q^2-2q+1)}{1+q+q^2} =4 13q^2-26q+13=4q^2+4q+4 9q^2-30q+9=0 \ \ | :3 3q^2-10q+3=0 D=100-36=64 q_1=\frac{10+8}{6} =\boxed{3} q_2=\frac{10-8}{6} =\frac{1}{3} \ ; \ q

Тогда

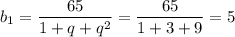
b_1=\dfrac{65}{1+q+q^2}=\dfrac{65}{1+3+9} =5

Нужно найти пятый член

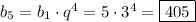
b_5=b_1\cdot q^4=5\cdot 3^4=\boxed{405 }

кошачка278
кошачка278
4,6(89 оценок)
Juru9a9wr0au92r902au9

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS