Регистрация Спросить otvet5GPT
алина200423
13.03.2022 00:44
Алгебра
Есть ответ 👍

в геометрической прогрессии известно, что b1+b4=27, b2+b3=18. Найдите первый член и знаменатель прогрессии

212
303
Посмотреть ответы 3

Ответы на вопрос:

youliya16
youliya16
4,8(79 оценок)

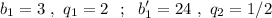
\displaystyle b_1=3 \ , \ q_1=2 \ \ ; \ \ b_1'=24 \ , \ q_2=1/2

Объяснение:

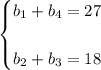
\displaystyle \begin{cases} b_1+b_4=27 b_2+b_3=18 \end{cases}

Воспользуемся формулами :

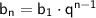
\sf \ b_n=b_1\cdot q^{n-1}

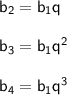
\sf \displaystye b_2=b_1q b_3=b_1q^2 b_4=b_1q^3  

Где b₁- первый член прогрессии ; q-знаменатель прогрессии

Подставим :

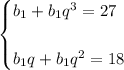
\displaystyle \begin{cases} b_1+b_1 q^3=27 b_1q+b_1q^2=18 \end{cases}

Вынесем за скобки общий  множитель :

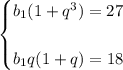
\displaystyle \begin{cases} b_1(1+q^3)=27 b_1q(1+q)=18 \end{cases}

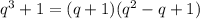
q^3+1=(q+1)(q^2-q+1)

Подставим и разделим

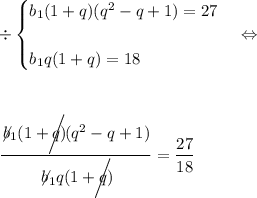
\div \displaystyle \begin{cases} b_1(1+q)(q^2-q+1)=27 b_1q(1+q)=18 \end{cases} \Leftrightarrow \frac{\not \!b_1(1+q) \!\!\!\!\!\!\!\bigg \slash(q^2-q+1)}{\not \!b_1q(1+q) \!\!\!\!\!\!\!\bigg \slash } =\frac{27}{18}

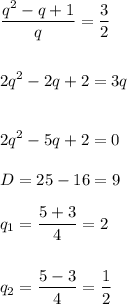
\displaystyle \frac{q^2-q+1}{q} =\frac{3}{2 } 2q^2-2q+2=3q 2q^2-5q+2=0 D=25-16=9 q_1=\frac{5+3}{4} =2 q_2=\frac{5-3}{4} =\frac{1}{2}

Тогда первый член будет принимать два различных значения :

Подставим q в данное уравнение

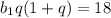
b_1q(1+q)=18

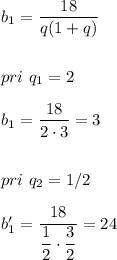
b_1=\dfrac{18}{q(1+q)} pri \ q_1=2 b_1=\dfrac{18}{2\cdot 3} =3 pri \ q_2=1/2 b_1'=\dfrac{18}{\dfrac{1}{2} \cdot\dfrac{3}{2} } =24

Patara1986
Patara1986
4,7(12 оценок)

ответ: знаменатель равен 2, первый член равен 3. См фото.

Объяснение:


в геометрической прогрессии известно, что b1+b4=27, b2+b3=18. Найдите первый член и знаменатель прог
adri121
adri121
4,4(94 оценок)

то есть значения 

f'(x)=4x^3-5 

f'(0)=0-5=-5

f'(1)=4-5=-1 

 

 

 

 

 

 

 

 

 

 

 

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS