Регистрация Спросить otvet5GPT
виолетта430
28.05.2020 15:37
Алгебра
Есть ответ 👍

При каких целочисленных значениях параметра a, система 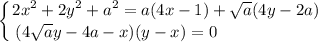\displaystyle \left \{ {{2x^2+2y^2+a^2=a(4x-1)+\sqrt{a}(4y-2a)} \atop {(4\sqrt{a}y-4a-x)(y-x)=0\qquad \qquad \qquad }} \right.
имеет нечётное число решений.

250
411
Посмотреть ответы 2

Ответы на вопрос:

smyslovgleb200
smyslovgleb200
4,7(78 оценок)

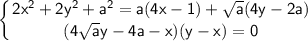
\displaystyle \sf \left \{ {{2x^2+2y^2+a^2=a(4x-1)+\sqrt{a}(4y-2a)} \atop {(4\sqrt{a}y-4a-x)(y-x)=0}} \right.

ОДЗ: a ≥ 0

Геометрия уравнений:

·  1-ое уравнение системы можно представить в виде

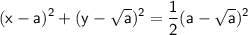
\displaystyle \sf (x-a)^2+(y-\sqrt{a})^2=\frac{1}{2}(a-\sqrt{a})^2

- это уравнение окружности с центром, движущимся по кривой y=√x и радиусом (a-√a)/√2.

·  2-ое уравнение - совокупность двух прямых

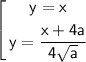
\left[ \begin{gathered} \sf y =x \\ \sf \displaystyle y=\frac{x+4a}{4\sqrt{a}} \\ \end{gathered} \right

1) Исследуем взаимное расположение первой прямой и окружности. Подставим y = x в первое уравнение системы. Получим квадратное уравнение:

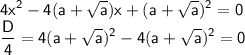
\sf \displaystyle 4x^2-4(a+\sqrt{a})x+(a+\sqrt{a})^2=0 \\ \frac{D}{4}=4(a+\sqrt{a})^2-4(a+\sqrt{a})^2=0

⇒  прямая y = x является касательной к окружности при любых a ≥ 0, что дает нам одно решение системы:

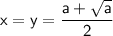
\sf \displaystyle x=y=\frac{a+\sqrt{a}}{2}

(!)  Заметим, что при a = 0 и a = 1 окружность вырождается в точку         (0, 0) и (1, 1) соответственно  ⇒  система имеет только одно решение при этих значениях a.

2)  Исследуем взаимное расположение второй прямой и окружности. Подставим y = (x+4a)/(4√a) в первое уравнение системы. Получим квадратное уравнение:

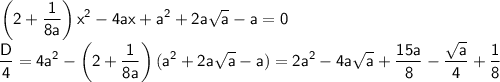
\sf \displaystyle \left(2+\frac{1}{8a}\right)x^2-4ax+a^2+2a\sqrt{a}-a=0 \\ \frac{D}{4}=4a^2-\left(2+\frac{1}{8a}\right)(a^2+2a\sqrt{a}-a)=2a^2-4a\sqrt{a}+\frac{15a}{8}-\frac{\sqrt{a}}{4}+\frac{1}{8}

Оценим дискриминант при значениях a = 2, a = 3, a ≥ 4:

·  a = 2

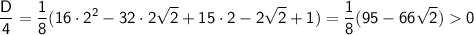
\sf \displaystyle \frac{D}{4}=\frac{1}{8}(16\cdot 2^2-32\cdot 2\sqrt{2}+15\cdot 2-2\sqrt{2}+1)=\frac{1}{8}(95-66\sqrt{2})0

т.к. 95/66 = (99 - 4)/66 = 1.5 - (2/33) > 1.5 - (7/100) = 1.43 > √2 ≈ 1.41

·  a = 3

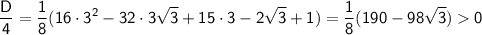
\sf \displaystyle \frac{D}{4}=\frac{1}{8}(16\cdot 3^2-32\cdot 3\sqrt{3}+15\cdot 3-2\sqrt{3}+1)=\frac{1}{8}(190-98\sqrt{3})0

т.к. 190/98 = (196-6)/98 = 2 - (6/98) > 2 - (7/100) = 1.93 > √3 ≈ 1.73

·  a ≥ 4

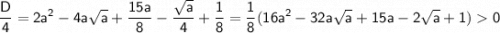
\sf \displaystyle \frac{D}{4}=2a^2-4a\sqrt{a}+\frac{15a}{8}-\frac{\sqrt{a}}{4}+\frac{1}{8}=\frac{1}{8}(16a^2-32a\sqrt{a}+15a-2\sqrt{a}+1)0

- очевидно, т. к.

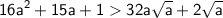
\sf \displaystyle 16a^2+15a+132a\sqrt{a}+2\sqrt{a}

ведь

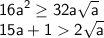
\sf \displaystyle 16a^2\geq 32a\sqrt{a} \\ 15a+1 2\sqrt{a}

Таким образом, при целочисленном a ≥ 2 прямая пересекает окружность в двух различных точках и, соответственно, дает 2 решения системы. Убедимся что они не совпадают с полученным ранее решением при целочисленных a. Для этого подставим x = y =     = (a + √a)/2 в уравнение y = (x + 4a)/(4√a), откуда найдем a = (33+5√41)/32 - не явл. целочисленным.

При a = 0 и a = 1 система имеет одно решение. При a ≥ 2, a ∈ Z система имеет 3 решения.

ответ: при любых целочисленных a ≥ 0.
КАЗ777
КАЗ777
4,5(12 оценок)

Потому-что 10 рублей * 30 купюр = 300

Самый подходящий вариант: 20р*20купюр + 10р*10купюр

Объяснение:

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS