Дано дифференциальное уравнение 1-го порядка и точка М. Определить тип дифференциального уравнения. Найти общее решение
дифференциального уравнения, уравнение интегральной кривой, проходящей
через точку М и уравнения еще 4-х интегральных кривых. Построить все эти
кривые в системе координат.
Пытаюсь решить это уже 4 дня. Внятного объяснения не могу найти. Получил 5 разных ответов
1 - корень из 2
2 - минус корень из 2
3- e в степени корень из 2
4 - 1/(e в степени корень из 2)
5 - модуль( корень из 2)

287

409

Посмотреть ответы 2

Ответы на вопрос:

adamadam

Математика

4,6(55 оценок)

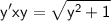
$\displaystyle \sf y'xy=\sqrt{y^2+1}$

Это уравнение с разделяющимися переменными.

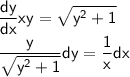
$\displaystyle \sf \frac{dy}{dx}xy=\sqrt{y^2+1} \\ \frac{y}{\sqrt{y^2+1}}dy=\frac{1}{x}dx$

Интегрируем уравнение. Для обеих частей уравнения считаем интегралы:

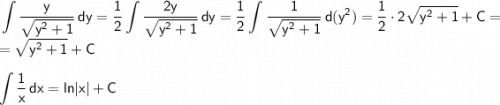
$\displaystyle \sf \int\limits {\frac{y}{\sqrt{y^2+1}}} \, dy= \frac{1}{2}\int\limits {\frac{2y}{\sqrt{y^2+1}}} \, dy=\frac{1}{2}\int\limits {\frac{1}{\sqrt{y^2+1}}} \, d(y^2)=\frac{1}{2}\cdot2\sqrt{y^2+1}+C=\\=\sqrt{y^2+1}+C \\ \\ \int\limits {\frac{1}{x}} \, dx =ln|x|+C$

Получим общее решение:

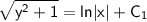
$\displaystyle \sf \sqrt{y^2+1}=ln|x|+C_1$

y(x) можно выразить явно:

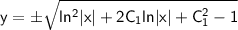
$\sf \displaystyle y=\pm\sqrt{ln^2|x|+2C_1ln|x|+C_1^2-1}$

Теперь найдем интегральную кривую, проходящую через точку M(1,1):

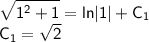
$\displaystyle \sf \sqrt{1^2+1}=ln|1|+C_1 \\ C_1=\sqrt{2}$

тогда

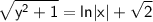
$\sf \displaystyle \sqrt{y^2+1}=ln|x|+\sqrt{2}$

- искомая интегральная кривая.

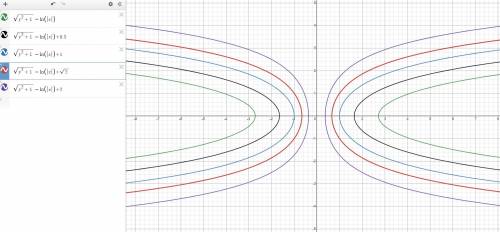
Другие интегральные кривые можно получать путем подстановки фиксированных значений вместо C₁. Примеры и их графики смотреть на картинке.

Дано дифференциальное уравнение 1-го порядка и точка М. Определить тип дифференциального уравнения.

sawbee

Математика

4,5(66 оценок)

Всем ! какая чудная пора к нам пришла и это - весна! и надо найти мисс весну, а ну-ка быстро угадай: кто это? ну? она затерялась между нами и прячется где-то в нас. не выманить её пирожками, но узнаете где она сейчас. я вам её найти. что для этот сделать? на конкурс придти? и кем я являюсь вам сказать? итак, я аня и я с орла. играть на инструментах обожаю я. могу вам спеть и станцевать и мисс весной готова стать! сойдёт? на уроке придумала)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.