точки E,F,M и K-середины соответственно рёбер AB, AD,CD и BC тетраэдра DABC,AC=14см, BD=6√ 2см, ME=√ 109 см. Найдите угол между прямыми AC и BD

234

341

Посмотреть ответы 1

Ответы на вопрос:

NicholasM

Геометрия

4,7(95 оценок)

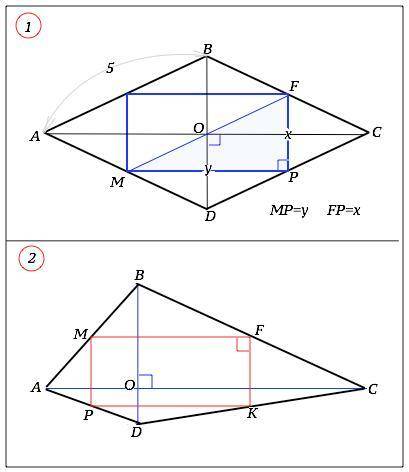
1) В ромбе ABCD точки F, P и M – середины сторон BC, CD, и AD соответственно. Найдите сумму длин диагоналей ромба, если АВ = 5 см, а периметр треугольника FPM равен 12 см.

————

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.

Так как точки F, P и M – середины сторон BC, CD и AD, отрезок FP — средняя линия ∆ BCD и равна половине диагонали ВD; МР - средняя линия ∆ АСD и равна половие диагонали АС.

FP║BD; MP║AC; a так как АС⊥ВD, то FP⊥МР. ⇒ ∆ MFP – прямоугольный.

Ромб - параллелограмм, все стороны ромба равны. Поэтому равны и их половины. BF=AM, ВF и АМ параллельны⇒

АВFM - параллелограмм, MF=AB=5 см.

Периметр ∆ MFP=5+FP+MP=12 (см) ⇒ FP+MP=12-5=7 (см)

Диагонали ромба вдвое больше катетов ∆ MFP, ⇒

BD+AC=2•( FP+MP)=2•7=14 (см).

—————

2) В четырехугольнике ABCD диагонали AC и BD перпендикулярны. Точки M, F, K и P – середины сторон АВ, BC, СD и DA соответственно. Докажите, что MK = FP.

Точки M, F, K и P – середины сторон четырехугольника ABCD, поэтому являются средними линиями треугольников АВС, ВСD, АСD и АВD. По свойству средней линии треугольника:

МР=FK и параллельны BD, а MF=P и параллельны АС.

АС⊥BD , ⇒ соседние стороны четырехугольника PMFK , которые им параллельны, взаимно перпендикулярны. PMFK - прямоугольник, МК и PF его диагонали. Диагонали прямоугольника равны. MK и FP – его диагонали. ⇒ MK = FP

ОЧЕНЬ НУЖНО 1) У ромбі ABCD точки F, P i M - середини сторін BC, CD, i AD відповідно. Знайдіть суму

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.