постройте в одной координатной плоскости графики функций y=-1/4x³, ТОЛЬКО ТАБЛИЦА КАК В ОБРАЗЦЕ, ГРАФИК НЕ НУЖЕН.
250
366
Ответы на вопрос:
Биквадратное уравнение.
Решается заменой переменной:
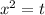
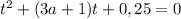
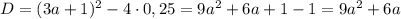
Если D >0, т.е.
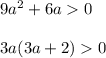
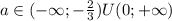
уравнение имеет корни:
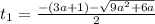 или
или 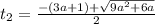
Обратный переход:
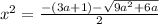 или
или 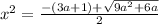
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
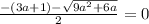
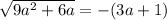
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:
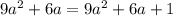
0=1 - неверно, нет таких значений а
Аналогично
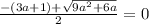
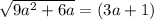
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:
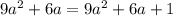
0=1 - неверно, нет таких значений а
Если 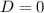 , т.е
, т.е 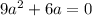
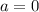 или
или 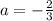
При 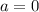
уравнение принимает вид:
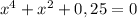
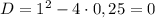 ⇒
⇒ 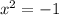
уравнение не имеет корней
При 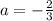
уравнение принимает вид:
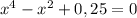
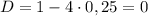 ⇒
⇒ 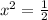
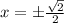
Уравнение 4-ой степени, значит
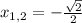 и
и 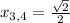
О т в е т. При 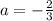
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Дана функция y=f(x), где f(x) =x^2 при каком значенииях аргумента верно равенство...
 Max325t10.07.2020 01:11
Max325t10.07.2020 01:11 -
Решите неравенство 9t^2-17 (3t-2)^2+15...
 HET22802.03.2023 04:11
HET22802.03.2023 04:11 -
Решите 40 решить дифференциальное уравнение первого порядка ydx=-xdy...
 Noora201703.04.2021 05:33
Noora201703.04.2021 05:33 -
Решить систему уравнений {2x+y=4 {x^2+y^2=5...
 pandapurple01.06.2020 04:34
pandapurple01.06.2020 04:34 -
1) решите неравенство 2) решите неравенство 3) решите неравенство...
 Sarzhanovaperuza13.11.2021 09:20
Sarzhanovaperuza13.11.2021 09:20 -
Найдите сторону cd треугольника bcd, если известно, что bc=4,bd=8,cosb=11/16...
 nesen0323.06.2022 00:12
nesen0323.06.2022 00:12 -
Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления,...
 sehya7219.04.2021 15:54
sehya7219.04.2021 15:54 -
Решительно уравнение 1).7x-9=40 2).найдите значение выражения 9b+5a-9b b при...
 dmgkmmsdk06.09.2021 08:32
dmgkmmsdk06.09.2021 08:32 -
Решить, ! 1) решите неравенство 2) найдите область определения выражения...
 YOP5622.06.2022 16:52
YOP5622.06.2022 16:52 -
Площадь треугольника,основание которого на 20 см. больше высоты,равна 78 см....
 nikitamarar217704.02.2022 15:21
nikitamarar217704.02.2022 15:21

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
