Регистрация Спросить otvet5GPT
Анастасия0411
21.12.2022 13:46
Геометрия
Есть ответ 👍

Докажите второй признак треугольника

159
335
Посмотреть ответы 3

Ответы на вопрос:

McBlanse
McBlanse
4,7(91 оценок)

Возьмём 2 треугольника

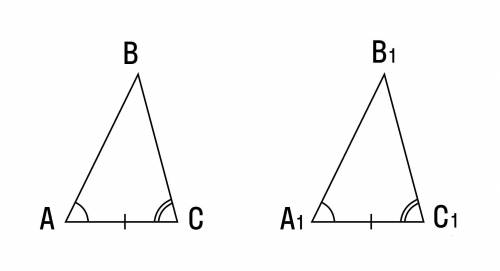
Нужно доказать, что △ABC  =  △A1B1C1.

Доказательство:

Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной  A1, вершины В и В1 лежат по одну сторону от А1С1.

АС совмещается с  A1C1, вершина C совпадает с C1

AB накладывается на A1B1

CB накладывается на C1B1

Вершина B совпадает с вершиной B1.

Если Всё совмещается => △ABC совмещается с △A1B1C1, значит, △ABC = △A1B1C1 .

по другому не докажешь)  


Докажите второй признак треугольника
Divas888
Divas888
4,5(80 оценок)
Второй признак равенства треугольников ?
если да , то
Теорема:
Если сторона и два прилегающих к ней угла одного треугольника соответственно равны стороне и двум прилежащих к ней углам другого треугольника то такие треугольники равны.
Дано: треугольник АВС и треугольник А1В1С1 ; АВ=А1В1; угол А= угол А1 , угол В = угол В1.
Доказать: треугольник АВС = треугольник А1В1С1.
Доказательства :
1) наложим АВ на А1В1 т.к. по условию АВ=А1В1 то вершины А и А1 ; В и В1 совпадут.
2) по условию угол А = угол А1 и угол В= угол В1 значит лучи АС и А1С1 ; ВС и В1С1 совпадут.
(.)С совпадёт с (.)С1 следовательно треугольники совпадут и треугольник АВС= треугольник А1В1С1.

Мой чертёж:
Докажите второй признак треугольника
sofiya13031
sofiya13031
4,4(7 оценок)
Так как вершины лежат в серединах сторон, то 5: 2=2,5 12: 2=6 14: 2=7  вот такие будут стороны

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS