Геометрия: Найти площадь параллелограмма

мпрьььоппааамт

24.11.2022 06:50

Геометрия

Есть ответ 👍

Найти площадь параллелограмма

190

440

Посмотреть ответы 2

Ответы на вопрос:

alikakusai35

Геометрия

4,4(48 оценок)

480,5 ед²

Объяснение:

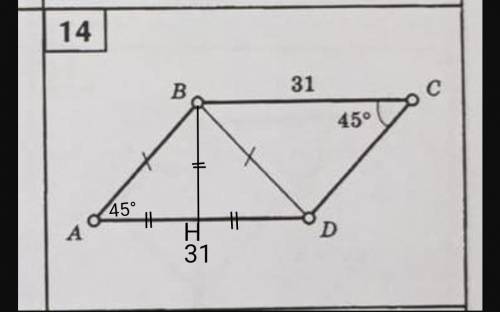
<А=<С=45°, свойство параллелограма

ВС=АD=31, свойство параллелограма

∆АВD- равнобедренный треугольник по условию

Проведем высоту ВН, которая будет также медиана и биссектрисса равнобедренного треугольника ∆АBD

AH=HD

AH=AD/2=31/2=15,5ед

∆АНВ- прямоугольный треугольник

Сумма острых углов в прямоугольном треугольнике равна 90°

<ВАD+<ABH=90° →

<ABH=90°-<BAD=90°-45°=45°

∆AHB- равнобедренный треугольник углы при основании равны.

АН=ВН.

S(ABCD)=BH*AD=15,5*31=480,5ед²

Кларесия10

Геометрия

4,5(55 оценок)

Пусть равс - данная пирамида, р-вершина, ро = √13 см - высота, ра=рв=рс=6 см 1. рассмотрим δ аор - прямоугольный. ао²+ро²=ра² - (по теореме пифагора) ао = √(ра²-ро²) = √(6² - (√13)²) = √(36-13) = √23 (см) 2. ао является радиусом описанной окружности. r=(a√3) / 3 a= (3r) / √3 = (3√23)/√3 = √69 (см) - это длина стороны основы. 3. находим периметр основы. р=3а р=3√69 см 4. проводим рм - апофему и находим ее. рассмотрим δ амр - прямоугольный. ам=0,5ав=0,5√69 см ам²+рм²=ра² - (по теореме пифагора) рм = √(ра²-ам²) = √(6² - (0,5√69)²) = √(36-17,25) = √18,75 = 2,5√3 (см) 5. находим площадь боковой поверхности пирамиды. р = 1/2 р₀l р = 1/2 · 3√69 · 2,5√3 = 3,75√207 = 3,75·3√23 = 11,25√23 (см²) ответ. 11,25 √23 см².

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.