Математика: Выполните действия: (7/12 - 1/3) * 16/19 (11/24 + 1/6)* 1 3/5

margaritavladim

04.09.2021 12:42

Математика

Есть ответ 👍

Выполните действия: (7/12 - 1/3) * 16/19
(11/24 + 1/6)* 1 3/5

213

461

Посмотреть ответы 1

Ответы на вопрос:

Darina17821

Математика

4,6(49 оценок)

Пошаговое объяснение:

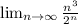
$\lim_{n \to \infty} \frac{n^3}{2^n}$

исследуем по признаку Даламбера

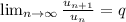
$\lim_{n \to \infty} \frac{u_{n+1}}{u_n } =q$

если q < 1, то ряд расходится, если q > 1, то сходится, если =1 неопределенность

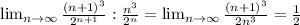
$\lim_{n \to \infty} \frac{(n+1)^3}{2^{n+1}} : \frac{n^3}{2^n} = \lim_{n \to \infty} \frac{(n+1)^3}{2n^3} = \frac{1}{2}$

ряд сходится

область сходимости ряда это [-R; R], где

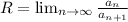
$R= \lim_{n \to \infty} \frac{a_n }{a_{n+1}}$

у нас 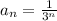$a_n = \frac{1}{3^n}$

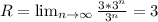
$R= \lim_{n \to \infty} \frac{3*3^n }{3^n}} = 3$

x₁ = 1-3 = -2

x₂ = 1+3 = 4

ряд абсолютно сходится при всех x ∈ (-2;4)

теперь на концах

х = -2

∑ 1/3ⁿ *(-3)ⁿ = (-1)ⁿ

знакочередующийся ряд

по первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего.

у нас 1=1=1 - не выполняется.

по второму признаку - предел ряда должен стремиться к нулю (при n стремящейся к бесконечности)

у нас 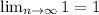$\lim_{n \to \infty} 1 = 1$

точка х = -2 есть точка расходимости

х = 4

исследуем при интегрального признака сходимости

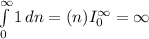
$\int\limits^ \infty}_0 {1} \, dn = (n) I_0^ \infty = \infty$

точка х = 4 так же точка расходимости

тут я не совсем уверена. вот что помню из института....

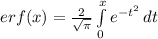
$erf(x) = \frac{2}{\sqrt{\pi } } \int\limits^x_0 {e^{-t^2}} \, dt$

так что, извините, если что не так

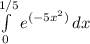
$\int\limits^{1/5}_0 {e^{(-5x^2)} \, dx$

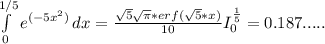
$\int\limits^{1/5}_0 {e^{(-5x^2)} \, dx = \frac{\sqrt{5} \sqrt{\pi} *erf(\sqrt{5}*x)}{10} I_0^{\frac{1}{5}} = 0.187.....$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.