лчлвоу

27.10.2022 22:21

Алгебра

Есть ответ 👍

1. Даны точки: A(-2;1), В(1;5) C(3;2). Постройте уголA,В,С, симметричный данному относительно оси
абсцисс. Запишите координаты точек А1,В1, С1?

122

205

Посмотреть ответы 2

Ответы на вопрос:

БОГДАН111153748854

Алгебра

4,5(2 оценок)

А 3;7 B 4;7,8 С 5;9

Объяснение:

держи хахпхахаха

началось1939

Алгебра

4,7(34 оценок)

(3;2)

(-3;-2)

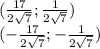
$(\frac{17}{2\sqrt{7}};\frac{1}{2\sqrt{7}} )\\(-\frac{17}{2\sqrt{7}};-\frac{1}{2\sqrt{7}} )$

Объяснение:

Умножим первое уравнение на 4 и сложим со вторым

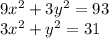
$9x^{2} +3y^{2} =93\\3x^{2} +y^{2} =31$

Выразим 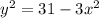$y^{2} =31-3x^{2}$ и подставим в первое уравнение

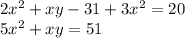
$2x^{2} +xy-31+3x^{2} =20\\5x^{2} +xy =51$

Подставим вместо y его представление 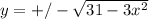$y=+/-\sqrt{31-3x^{2}}$

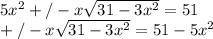
$5x^{2} +/-x\sqrt{31-3x^{2} } =51\\+/-x\sqrt{31-3x^{2} } =51-5x^{2}$

Возведем в последнем уравнении левую и правую часть в квадрат

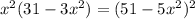
$x^{2} (31-3x^{2} )=(51-5x^{2} )^{2}$

Делаем замену 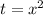$t=x^{2}$

В итоге приходим к квадратному уравнению

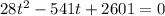
$28t^{2}-541t+2601=0$

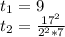
$t_{1}=9 \\t_{2}=\frac{17^{2} }{2^{2}*7 }$

Тогда 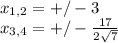$x_{1,2} =+/-3\\x_{3,4}=+/-\frac{17}{2\sqrt{7} }$

Вспоминая, что 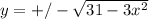$y=+/-\sqrt{31-3x^{2}}$ находим y

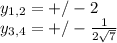
$y_{1,2}=+/-2 \\y_{3,4}=+/-\frac{1}{2\sqrt{7} }$

Для отбора правильных решений воспользуемся уравнением

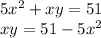
$5x^{2} +xy =51\\xy =51-5x^{2}$

Подставляя вместо 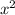$x^{2}$ его значения 9 и $\frac{289}{28}$ , определяем, что xy0

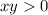
Значит x и y должны быть одного знака.

(3;2)

(-3;-2)

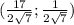
$(\frac{17}{2\sqrt{7}};\frac{1}{2\sqrt{7}} )$

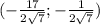
$(-\frac{17}{2\sqrt{7}};-\frac{1}{2\sqrt{7}} )$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.