Ответы на вопрос:
1) (1,75; 5,75)
2) (3; 3)
3) у = 7х
Объяснение:
Точкой пересечения графиков функций будет точка, (х,у), подходящая для обоих равенств.
То есть строго говоря это такая точка (х, у), где х и у являются решением системы уравнений:
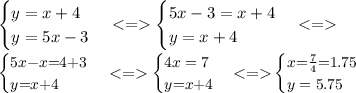
И искомые координаты точки будут (1,75; 5,75)
Можно решить проще:
Чтобы найти абсциссу (х) точки пересечения, приравняем
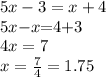
А ординату (у) точки пересечения найдем, подставив найденное значение (х) в любое из уравнений:
Например, в y = x + 4
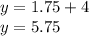
И искомые координаты точки будут (1,75; 5,75)
ответ (1,75; 5,75)
2.
Найти точку графика, абсцисса которой равна ординате
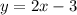
То есть требуется найти такую точку (х,у) графика,
у которой х = у.
Строго говоря, тут также требуется решение системы:
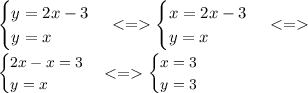
Это как бы пересечение двух графиков:
у = 2х - 3 и у = х
Но можно и проще.
Найти точку графика, абсцисса которой равна ординате, т.е. у = х.
Значит, подставляем х вместо у в уравнение;
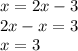
А так как по условию у = х, то
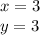
И искомые координаты точки будут (3; 3)
ответ: (3; 3)
3.
График линейной функции проходит через начало координат (т.е. точку О(0; 0)) и точку А(3; 21)
Следовательно, уравнение имеет форму
y = kx + b
причем т.к. график проходит через (0;0), следовательно
у(0) = 0 => 0 = k•0 + b <=> b = 0
а значит уравнение прямой имеет форму:
y = kx + 0 <=> y = kx
И т.к. график проходит через А(3; 21), следовательно
у(3) = 21 <=> k•3 = 21 <=> k = 21:3
k = 7
Итак, получили, что b = 0; k = 7
А значит уравнение примет вид:
у = 7х
ответ: у = 7х
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Y=-2x^2-8x-2,5 постройте график функции. , 30...
 etyan0015.11.2020 20:45
etyan0015.11.2020 20:45 -
Решить неравенство (х-2)^2 ≤ х (х-3)+8 сегодня...
 nairchik14.03.2023 08:36
nairchik14.03.2023 08:36 -
2^(2x-1) - 7*2^(x-1) + 5 ≤ 0 друзья! кто сможет подробно объяснить один...
 dis805.04.2023 07:23
dis805.04.2023 07:23 -
График функции y=6x−3 пересекает ось oyв точке с координатами: ...
 alinkass27.07.2020 14:17
alinkass27.07.2020 14:17 -
В4 найдите одз. рассмотрите отдельно случай, при каких а в одз исключаются...
 Morij00714.02.2021 19:07
Morij00714.02.2021 19:07 -
Исследовать, начертить таблицу и построить график. y=2x^2+5x+2...
 Masha2008260623.05.2020 04:52
Masha2008260623.05.2020 04:52 -
Найти значение выражения 5cos² x +1 ,если sin²x =0,3...
 egorshlyahov12p0dhm923.02.2022 01:14
egorshlyahov12p0dhm923.02.2022 01:14 -
Преобразуйте в многочлен выражение : (a+b)^2(a-b) сократите дробь:...
 asdf3716.07.2020 22:51
asdf3716.07.2020 22:51 -
«поезд проходит расстояние между за 8 часов. если он увеличит скорость...
 evseeva09060118.03.2022 06:21
evseeva09060118.03.2022 06:21 -
=** четыре года назад завод изготовил 10 000единиц некоторого изделия...
 Анжеkf2304.05.2022 22:05
Анжеkf2304.05.2022 22:05

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

![x\in(-\infty; 5]\cup[-4; 0]\cup[4; +\infty)](/tpl/images/3780/7132/64da2.png)
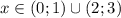
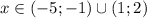
![x\in(-\infty;-7]\cup(-5; 1]\cup(5; +\infty)](/tpl/images/3780/7132/bc807.png)
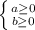 или
или 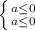
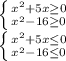
![\left \{ {{x\in(-\infty;-5]\cup[0; +\infty)} \atop {x\in(-\infty;-4]\cup[4; +\infty)}} \right. \\\left \{ {{x\in[-5;0]} \atop {x\in[-4;4]}} \right.](/tpl/images/3780/7132/3ca81.png)
![x\in(-\infty; -5]\cup(4; +\infty)\\x\in[-4;0]](/tpl/images/3780/7132/5c5ce.png)