Задача по правилу Лопиталя. Понимаю что нужно записать в качестве натурального логаритма, но получаю бесконечность/0 и немогу применить теорему лопиталя

249

272

Посмотреть ответы 2

Ответы на вопрос:

Ромашка111113

Математика

4,7(35 оценок)

Пошаговое объяснение:

$\lim _{x \to0} \big((2x)^{tg \: {x}} \big) = \left[ {0}^{0} \right] = \lim _{x \to0} { e}^{ \ln\left((2x)^{tg \: {x}} \right)} = \\ = \lim _{x \to0} { e}^{ tg \: {x} {\cdot}\ln(2x) } = { e}^{\lim _{x \to0} (tg \: {x} {\cdot}\ln(2x)) } = \\$

Здесь ключевой момент!

Мы неопределенность [tg • ln] или [бскнч • 0]

преобразуем по формуле:

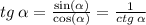
$tg \: \alpha = \frac{ \sin( \alpha ) }{ \cos( \alpha ) } = \frac{1}{ctg \: \alpha } \\$

т.к. функция тангенс это же (1 / котангенс)!

Потом - правило Лопиталя.

$\: = {\lim _{x \to0} (tg \: {x} {\cdot}\ln(2x)) } =\left[ \infty \cdot0 \right] = \\ = {\lim _{x \to0} \frac{\ln2x}{ctg \: {x}} } =\left[ \frac{0}{0} \right] = \lim _{x \to0} \frac{(\ln2x)'}{(ctg \: {x})'} = \\ = \large \lim _{x \to0} \small{\: \frac{ \dfrac{2}{2x} }{- \dfrac{1}{ \sin^{2}x } } } = \large \lim _{x \to0} \small{\: - \frac{2\sin^{2}x}{2x } } = \\ - \lim _{x \to0} \small{\: \frac{\sin^{2}x}{x } } =\left[ \: \frac{0}{0} \: \right] =... \\$

Еще раз правило Лопиталя:

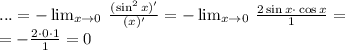
$\\... = - \lim _{x \to0} \small{\: \frac{(\sin^{2}x)'}{(x )'} } =- \lim _{x \to0} \small{\: \frac{2\sin{x}{ \cdot}\cos{x}}{1} } =\\ = - \frac{2 \cdot0 \cdot1}{1} = 0 \\$

GeliaSecret2005

Математика

4,6(53 оценок)

Точки B и D противоположные, так как координата у точки В(-7,5),а у точки D(7,5), то есть они находятся на равном расстоянии от нуля, ну или же к координате точки B просто прибавили "-", всё...За еденичный отрезок естественно взяла 1 см/2 клетки.. Потому что, если возьмёшь ед.отрезок за 0,5 см/одна клетка у тебя там каша будет, так как числа не целые..

A)на кординатной прямой отметьте точки A(-5).B(-7,5).C(2,5).D(7,5) б)Укажите точки с противоположным

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.