Регистрация Спросить otvet5GPT
kirushaaa
10.03.2020 16:24
Алгебра
Есть ответ 👍

найти координаты проекции точки А=(4;7;7) на плоскость, заданную уравнением 3х+2у+2z+11=0

204
359
Посмотреть ответы 2

Ответы на вопрос:

Enot787
Enot787
4,4(18 оценок)

(-5; 1; 1)

Объяснение:

Найдём уравнение прямой, перпендикулярной данной плоскости и проходящей через точку A. Направляющим вектором данной прямой является вектор нормали плоскости, то есть вектор {3; 2; 2}. Составим каноническое уравнение прямой:

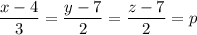
\dfrac{x-4}{3}=\dfrac{y-7}{2}=\dfrac{z-7}{2}=p

Из этого уравнения составим параметрическое уравнение:

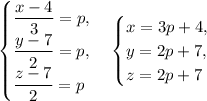
\begin{cases}\dfrac{x-4}{3}=p,\\ \dfrac{y-7}{2}=p,\\ \dfrac{z-7}{2}=p\end{cases}\begin{cases}x=3p+4,\\ y=2p+7,\\ z=2p+7\end{cases}

Чтобы найти точку пересечения прямой с плоскостью, то есть проекцию данной точки, подставим координаты из параметрического уравнения в уравнение плоскости:

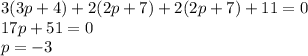
3(3p+4)+2(2p+7)+2(2p+7)+11=0\\17p+51=0\\p=-3

Подставляя найденное значение параметра, получим координаты искомой точки:

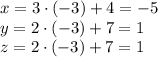
x=3\cdot(-3)+4=-5\\y=2\cdot (-3)+7=1\\z=2\cdot (-3)+7=1

lavika1
lavika1
4,6(45 оценок)
(a²-5)²-(2a+3)²=0 (a²-5-2a-3)(a²-5+2a+3)=0 (a²-2a-8)(a²+2a-2)=0 a²-2a-8=0 a1+a2=2 u a1*a2=-8 a1=-2 u a2=4 a²+2a-2=0 d=4+8=12 a3=(-2-2√3)/2=-1-√3 a2=-1+√3

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS