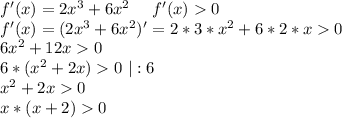Регистрация Спросить otvet5GPT
proovdnik
02.03.2022 21:26
Алгебра
Есть ответ 👍

Решите неравенство f '(x)>0, если f(x)=2x³+6х²

295
363
Посмотреть ответы 3

Ответы на вопрос:

26Violetta26
26Violetta26
4,8(65 оценок)

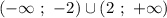
(-\infty \ ; \ -2) \cup (2 \ ; \ +\infty)

Объяснение:

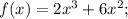
f(x)=2x^{3}+6x^{2};

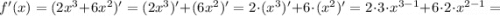
f'(x)=(2x^{3}+6x^{2})'=(2x^{3})'+(6x^{2})'=2 \cdot (x^{3})'+6 \cdot (x^{2})'=2 \cdot 3 \cdot x^{3-1}+6 \cdot 2 \cdot x^{2-1}=

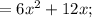
=6x^{2}+12x;

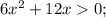
6x^{2}+12x0;

x^{2}+2x0;

Найдём нули функции:

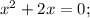
x^{2}+2x=0;

x(x+2)=0;

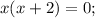
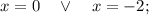
x=0 \quad \vee \quad x+2=0;

x=0 \quad \vee \quad x=-2;

Определим знаки неравенства на промежутках

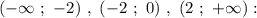
(-\infty \ ; \ -2) \ , \ (-2 \ ; \ 0) \ , \ (2 \ ; \ +\infty):

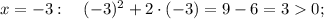
x=-3: \quad (-3)^{2}+2 \cdot (-3)=9-6=30;

x=-1: \quad (-1)^{2}+2 \cdot (-1)=1-2=-1

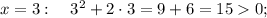
x=3: \quad 3^{2}+2 \cdot 3=9+6=150;

Неравенство принимает положительные значения на промежутках

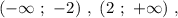
(-\infty \ ; \ -2) \ , \ (2 \ ; \ +\infty) \ ,

значит,

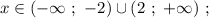
x \in (-\infty \ ; \ -2) \cup (2 \ ; \ +\infty) \ ;

sonia81
sonia81
4,6(58 оценок)

Объяснение:

f'(x)=2x^3+6x^2 \ \ \ \ f'(x)0\\f'(x)=(2x^3+6x^2)'=2*3*x^2+6*2*x0\\6x^2+12x0\\6*(x^2+2x)0\ |:6\\x^2+2x0\\x*(x+2)0\\

-∞__+__-2__-__0__+__+∞           ⇒

ответ:x∈(-∞;-2)U(0;+∞).

Dog7771
Dog7771
4,4(27 оценок)
Если бы вы показали графики, я мог бы сказать (написать).

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS