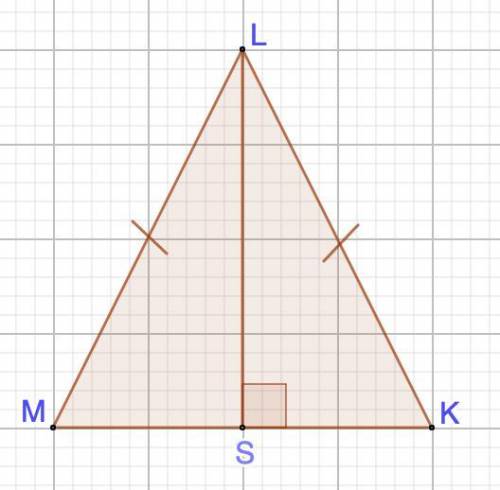
РЕБЯТ В равнобедренном треугольнике LMK, с основанием MK, проведена высота LS.

Докажите, что треугольник LSM равен треугольнику LSK, используя:

1) 2 признак равенства треугольников

2) 3 признак равенства треугольников

156

485

Посмотреть ответы 2

Ответы на вопрос:

liona676

Геометрия

4,7(66 оценок)

Объяснение:

Дано: ΔLMK - равнобедренный.

МК - основание.

LS - высота

Доказать: ΔLSM = ΔLSK, используя 2 и 3 признаки равенства треугольников.

Доказательство:

1) 2 признак равенства треугольников:

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники называются равными.

Рассмотрим ΔLSM и ΔLSK - прямоугольные (LS - высота)

⇒ ∠LSM = ∠LSK = 90°

В равнобедренном треугольнике высота является биссектрисой.

⇒ ∠MLS = ∠SLK

LS - общая

⇒ ΔLSM = ΔLSK (по 2 признаку)

2) 3 признак равенства треугольников:

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники называются равными.

Рассмотрим ΔLSM и ΔLSK - прямоугольные (LS - высота)

В равнобедренном треугольнике высота является медианой.

⇒ MS = SK

ML = LK (ΔLMK - равнобедренный)

LS - общая

⇒ ΔLSM = ΔLSK (по 3 признаку)

РЕБЯТ В равнобедренном треугольнике LMK, с основанием MK, проведена высота LS.Докажите, что треуголь

Рапиро123

Геометрия

4,7(90 оценок)

Х- первый угол 11х- второй угол сумма смежных углов=180 градусов⇒11х+х=180 12х=180 х=15 градусов - первый угол второй угол=15*11=165 градусов

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.