Математика: (x+3)(6-x)(x-2)(x+4)+126x^2=0

Neznаykа

28.03.2022 04:17

Математика

Есть ответ 👍

(x+3)(6-x)(x-2)(x+4)+126x^2=0

108

362

Посмотреть ответы 2

Ответы на вопрос:

Tipaniktuta

Математика

4,5(33 оценок)

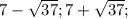
$7-\sqrt{37} ; 7+\sqrt{37};$ -12; -1.

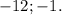
Пошаговое объяснение:

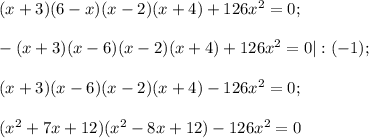
$(x+3)(6-x)(x-2)(x+4)+126x^{2} =0;-(x+3)(x-6)(x-2)(x+4)+126x^{2} =0|:(-1);(x+3)(x-6)(x-2)(x+4)-126x^{2} =0;(x^{2} +7x+12)(x^{2} -8x+12)-126x^{2} =0$

Так как 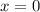x=0 не является корнем полученного уравнения, то разделим обе части уравнения на $x^{2}$ .

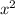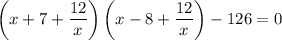
$\left(x+7+\dfrac{12}{x}\right )\left( x-8+\dfrac{12}{x}\right )-126=0$

Пусть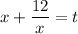 $x+\dfrac{12}{x} =t$ , тогда уравнение принимает вид:

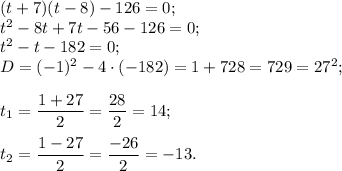
$(t+7)(t-8)-126=0;\\t^{2} -8t+7t-56-126=0;\\t^{2}-t- 182=0;\\D= (-1) ^{2} -4\cdot(-182)= 1+728=729=27^{2} ;t{_1}= \dfrac{1+27}{2} =\dfrac{28}{2} =14;t{_2}= \dfrac{1-27}{2} =\dfrac{-26}{2} =-13.$

Вернемся к замене и получим:

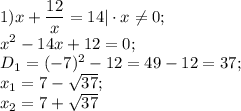
$1) x+\dfrac{12}{x} =14|\cdot x\neq 0;\\x^{2} -14x+12=0;\\D{_1}= (-7) ^{2} -12=49-12=37;\\x{_1}= 7-\sqrt{37} ;\\x{_2}= 7+\sqrt{37}$

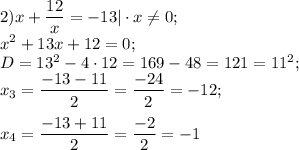
$2)x+\dfrac{12}{x} =-13|\cdot x\neq 0;\\x^{2} +13x+12=0;\\D= 13 ^{2} -4\cdot12=169-48=121=11^{2} ;\\x{_3}= \dfrac{-13-11}{2}=\dfrac{-24}{2} =-12 ;x{_4}= \dfrac{-13+11}{2}=\dfrac{-2}{2} =-1$

KristinkaVayyyys

Математика

4,5(49 оценок)

11+2,3*y+1,3*y=3811+3,6у=383,6у=27у=7,5

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.