Задание 1. К уравнению 2x – 3(y – 1) + 2 = 0 подберите второе уравнение так, чтобы полученная система уравнений:
а) имела бесконечное множество решений ( );
б) не имела решений ( ).
284
373
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Первую половину пути автомобиль проехал со скоростью 85 км/ч, а вторую- со...
 sxxaaa29.04.2021 06:16
sxxaaa29.04.2021 06:16 -
Первое уравнение системы имеет вид 7х-15у=3. второе уравнение имеет вид ах+10у=с....
 varzhyv26.02.2022 07:45
varzhyv26.02.2022 07:45 -
Выражение (а+2) в квадрате - а(4-7а) найдите его значение при a= -1/2 (дробь)...
 tanyakozina0009.04.2022 04:38
tanyakozina0009.04.2022 04:38 -
Выражение: a)3a^2+6ab+3b^2 б)a^3-4a...
 vztositgicgc18.07.2021 23:55
vztositgicgc18.07.2021 23:55 -
Решить неравенство,изобразить решение неравенства на числовой \ прямой и записать...
 katasmajl26.11.2022 17:19
katasmajl26.11.2022 17:19 -
Одне число менше від іншого на 20 а їх добуток дорівнює -91. знайдіть ці числа...
 handofkremlin19.07.2022 05:09
handofkremlin19.07.2022 05:09 -
Решите, , данное уравнение 4(x-1)^2=9(x+1)^2(x-3)^2(4-x)(x+2) ещё ни разу мне...
 Емсимася23.06.2021 11:42
Емсимася23.06.2021 11:42 -
7. Запишите в виде выражения: 1) сумму выражений 4т и 7k; 2) квадрат разности...
 12251928.01.2022 12:37
12251928.01.2022 12:37 -
Задание 1 ( ). Раскройте скобки и упростите выражение: -4/18(2 7/10a-1,5b)...
 данил208017.11.2020 09:31
данил208017.11.2020 09:31 -
Решите системы уравнений {х+у=6 ху=8...
 kalmuratov7005.01.2021 19:13
kalmuratov7005.01.2021 19:13

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

![\left \{ {{\sqrt[3]{x+2y}+\sqrt[3]{x-y+2}=3 } \atop {2x+y=7}} \right.](/tpl/images/4978/3322/4d12f.png)
![\left \{ {{\sqrt[3]{x+2y}+\sqrt[3]{x-y+2}=3 } \atop {y=7-2x}} \right.](/tpl/images/4978/3322/991ca.png)
![\left \{ {{\sqrt[3]{x+14-4x}+\sqrt[3]{x-7+2x+2}=3 } \atop {y=7-2x}} \right.](/tpl/images/4978/3322/27a4f.png)
![\left \{ {{\sqrt[3]{14-3x}+\sqrt[3]{3x-5}=3 } \atop {y=7-2x}} \right.](/tpl/images/4978/3322/4f623.png)
![\sqrt[3]{14-3x} =a , 14-3x=a^3](/tpl/images/4978/3322/04d44.png) , a
, a ![\sqrt[3]{3x-5} =b, 3x-5=b^3](/tpl/images/4978/3322/393f8.png) ;
;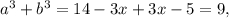 при чому
при чому 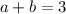
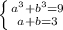
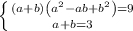
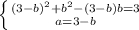
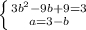
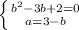
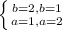
![\left \{ {{\sqrt[3]{14-3x} =1} \atop {\sqrt[3]{3x-5} =2}} \right.](/tpl/images/4978/3322/d1ed0.png) або
або ![\left \{ {{\sqrt[3]{14-3x} =2} \atop {\sqrt[3]{3x-5} =1}} \right.](/tpl/images/4978/3322/f0735.png)
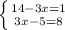 або
або 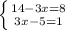
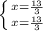 або
або 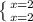
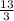 ,
,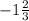 )
)