Kotik5l6

24.01.2020 20:01

Геометрия

Есть ответ 👍

В треугольнике ABC отрезок AD, проведенный из вершины A к стороне BC, делит последнюю в отношении 2:3. Из вершины B к стороне AC проведен отрезок BE, который пересекается с отрезком AD в точке Q так, что BQ = 2QE. Найти, в каком отношении точка E делит сторону AC. дайте ответ с решением .

170

336

Посмотреть ответы 2

Ответы на вопрос:

Миша75040406

Геометрия

4,8(64 оценок)

АЕ : ЕС = 1 : 2

Объяснение:

Проведем BF║AС.

ΔBFD ~ ΔCAD по двум углам (∠BFD = ∠CAD как накрест лежащие при пересечении параллельных прямых BF и АС секущей AF, углы при вершине D равны, как вертикальные).

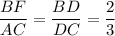
$\dfrac{BF}{AC}=\dfrac{BD}{DC}=\dfrac{2}{3}$

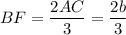
$BF=\dfrac{2AC}{3}=\dfrac{2b}{3}$

ΔBQF ~ ΔEQA по двум углам (∠BFD = ∠CAD, углы при вершине Q равны как вертикальные)

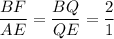
$\dfrac{BF}{AE}=\dfrac{BQ}{QE}=\dfrac{2}{1}$

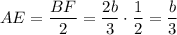
$AE=\dfrac{BF}{2}=\dfrac{2b}{3}\cdot \dfrac{1}{2}=\dfrac{b}{3}$

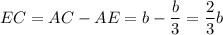
$EC=AC-AE=b-\dfrac{b}{3}=\dfrac{2}{3}b$

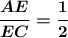
$\boldsymbol{\dfrac{AE}{EC}=\dfrac{1}{2}}$

Задачу можно решить проще, применив теорему Менелая для ΔЕВС:

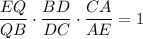
$\dfrac{EQ}{QB}\cdot \dfrac{BD}{DC}\cdot \dfrac{CA}{AE}=1$

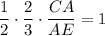
$\dfrac{1}{2}\cdot \dfrac{2}{3}\cdot \dfrac{CA}{AE}=1$

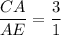
$\dfrac{CA}{AE}=\dfrac{3}{1}$

Отсюда следует, что

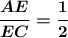
$\boldsymbol{\dfrac{AE}{EC}=\dfrac{1}{2}}$

В треугольнике ABC отрезок AD, проведенный из вершины A к стороне BC, делит последнюю в отношении 2:

Aislu111

Геометрия

4,7(60 оценок)

1) 2

2) 1

3)1

Объяснение:

sin²a+cos²a= 1

1+1=2

2) 1-cos²a=sin²a

3) 1-sin²a=cos²a

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.