01.02.2020 02:58

Есть ответ 👍

Докажи, что четырёхугольник ABCD, вершины которого имеют координаты A(14;3), B(26;7), C(22;19) и D(10;15), является квадратом; найди его площадь. SABCD=
.

182

344

Посмотреть ответы 2

Ответы на вопрос:

RUMBANITTA

Математика

4,5(48 оценок)

Дано: A(14;3); B(26;7); C(22;19); D(10;15).

Решение.

1) Найдём стороны четырёхугольника ABCD.

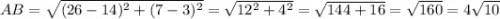
$AB=\sqrt{(26-14)^2+(7-3)^2}=\sqrt{12^2+4^2}=\sqrt{144+16}=\sqrt{160}=4\sqrt{10}$

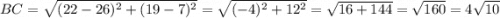
$BC=\sqrt{(22-26)^2+(19-7)^2}=\sqrt{(-4)^2+12^2}=\sqrt{16+144}=\sqrt{160}=4\sqrt{10}$

$CD=\sqrt{(10-22)^2+(15-19)^2}=\sqrt{12^2+4^2}=\sqrt{144+16}=\sqrt{160}=4\sqrt{10}$

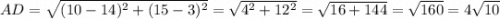
$AD=\sqrt{(10-14)^2+(15-3)^2}=\sqrt{4^2+12^2}=\sqrt{16+144}=\sqrt{160}=4\sqrt{10}$

Стороны четырёхугольника ABCD равны между собой.

2) Найдём диагонали четырёхугольника ABCD.

$AC=\sqrt{(22-14)^2+(19-3)^2}=\sqrt{8^2+16^2}=\sqrt{64+256}=\sqrt{320}=8\sqrt{5}$

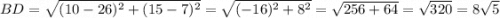
$BD=\sqrt{(10-26)^2+(15-7)^2}=\sqrt{(-16)^2+8^2}=\sqrt{256+64}=\sqrt{320}=8\sqrt{5}$

Диагонали четырёхугольника ABCD равны между собой.

3) Если стороны четырёхугольника ABCD равны между собой и его диагонали равны между собой, значит, четырёхугольник ABCD - квадрат.

Доказано.

4) Найдём 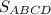$S_{ABCD}$ - площадь квадрата ABCD.

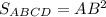
$S_{ABCD} =AB^2$

$S_{ABCD} =(4\sqrt{10} )^2=160$

$S_{ABCD} =160$

ответ: $S_{ABCD} =160$

anisinivan09p08i87

Математика

4,6(77 оценок)

Первый путешественник прошел пешком ровно половину пути, а вторую половину проехал на автобусе. второй же прошел сколько-то времени и за это же время проехал на автобусе. скорость автобуса превышает скорость человека и поэтому можно предположить, что большую часть пути второй путешественник проехал. на основе этого можно сделать вывод, что он добрался раньше первого до назначенного места. ответ: второй путешественник

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.