tarantilla

06.07.2022 21:53

Есть ответ 👍

Задание 1. НУЖЕН РИСУНОК

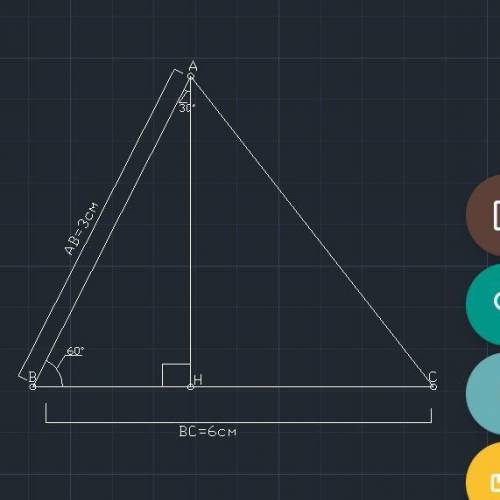
Две стороны треугольника равны 3 см и 6 см, а угол между ними составляет 60°. Определите:

а) длину третьей стороны треугольника ( );

б) периметр треугольника ( );

в) площадь треугольника ( );

г) радиус окружности, описанной около треугольника ( ).

ЛЮДИ ДОБРЫЕ МНЕ НЕ НУЖНО РЕШЕНИЕ МНЕ НУЖЕН РИСУНОК

294

374

Посмотреть ответы 2

Ответы на вопрос:

незнайка1162

Геометрия

4,8(68 оценок)

а) Опустим высоту АН из вершины угла, и рассмотрим получившийся прямоугольный треугольник АВН,

{< - угол}

<Н=90°, по определению прямоугольного треугольника, зная сумму всех углов этого треугольника, найдем <ВАН

<ВАН=90°-60°=30°

Против угла в 30° лежит катет равный половине гипотенузы, а значит ВН=0,5*3=1,5

Найдем АН по теореме Пифагора

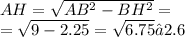
$AH = \sqrt{ AB {}^{2} - BH {}^{2} } = \\ = \sqrt{9 - 2.25} = \sqrt{6.75} ≈2.6$

Найдем НС, зная ВН и ВС,

HC = 6 - 1.5 = 4.5

Рассмотрим треугольник АСН, прямоугольный,

Отсюда,

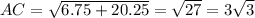
$AC= \sqrt{6.75 + 20.25 } = \sqrt{27} =3\sqrt{3}$

б) Периметр треугольника равен сумме сторон,

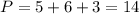
P = 5 + 6 + 3 = 14

в)Площадь треугольника равна половине произведения АВ на НС и на SinB

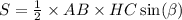
$S= \frac{1}{2} \times AB \times HC \sin( \beta )$

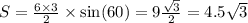
$S= \frac{6 \times 3}{2} \times \sin(60) = 9 \frac{ \sqrt{3} }{2} = 4.5 \sqrt{3}$

или

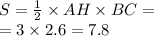
$S= \frac{1}{2} \times AH \times BC = \\ = 3 \times 2.6 = 7.8$

г) Радиус окружности можно вывести из формулы

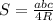
$S= \frac{abc}{4 R }$

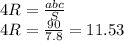
$4R = \frac{abc}{S } \\ 4R = \frac{90}{7.8} = 11.53$

$R = \frac{11.53}{4} = 2.88$

мака2007

Геометрия

4,6(99 оценок)

Периметр треугольника равен 18 см

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.