Регистрация Спросить otvet5GPT
Marína19112006
22.10.2021 02:27
Алгебра
Есть ответ 👍

: ( х-1 )|х²+1| + |х-1| (х²+1) = 0

229
371
Посмотреть ответы 3

Ответы на вопрос:

Полинаed
Полинаed
4,4(3 оценок)

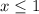
x\leq 1

Объяснение:

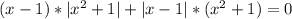
( x-1 )*|x^{2} +1| + |x-1|* (x^{2} +1) = 0

х²+1 всегда больше нуля, значит просто опускаем модуль

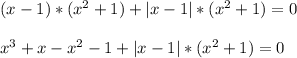
( x-1 )*(x^{2} +1) + |x-1|* (x^{2} +1) = 0 x^{3} +x-x^{2} -1+|x-1|*(x^{2}+1) = 0

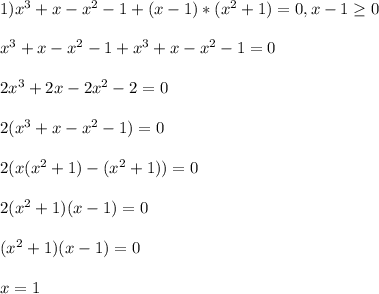
1)x^{3} +x-x^{2}-1+(x-1)*(x^{2}+1) = 0, x - 1 \geq 0x^{3} +x-x^{2}-1+x^{3} +x-x^{2} -1=02x^{3}+2x-2x^{2}-2=02(x^{3} +x-x^{2} -1)=02(x(x^{2} +1)-(x^{2} +1))=02(x^{2} +1)(x-1)=0(x^{2} +1)(x-1)=0x = 1        

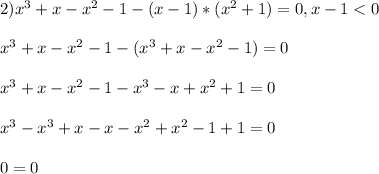
2) x^{3} +x-x^{2}-1-(x-1)*(x^{2}+1) = 0, x - 1

x-1    

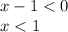
Объединяем:

x=1\\x

ответ: x\leq 1

Brauberg898117
Brauberg898117
4,4(51 оценок)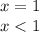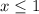

ответ:     хЄ (- ∞ ; 1 ] .

Объяснение:

( x - 1 )| x² + 1 | + | x - 1 |(  x² + 1 ) = 0 ;

( x - 1 )( x² + 1 ) + | x - 1 |(  x² + 1 ) = 0 ;

( x² + 1 )( x - 1 + | x - 1 | ) = 0 ;

x² + 1 ≠ 0      або    x - 1 + | x - 1 |  = 0 ;  

розв"язуємо останнє рівняння :

| x - 1 |  = - х + 1 ;

вираз під модулем дорівнює  0  при  х = 1 .

1) х ≤ 1  , тоді  - ( x - 1 ) = - ( x - 1 ) ;  правильна рівність при хЄ (- ∞ ; 1 ] ;

2) x > 1 , тоді   x - 1 = - х + 1 ;  > 2x = 2 ;  > x = 1 ∉ ( 1 ; + ∞ ) .

В - дь :    хЄ (- ∞ ; 1 ] .

lizochkanaumov1
lizochkanaumov1
4,7(12 оценок)
Коли знаменник дорівнює нулю.         при значенні n=2  вираз не має змісту.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS