Регистрация Спросить otvet5GPT
Vasya1337ez
02.12.2022 08:34
Алгебра
Есть ответ 👍

Числовая окружность. Кто может пояснить почему мы берём именно 3 углов прямых и добавляем их к сумме , и как их найти?, если считать без калькулятора возможно их найти самому, объясните как?.

297
407
Посмотреть ответы 2

Ответы на вопрос:

Mojo228
Mojo228
4,6(51 оценок)

Так как при вращении на 360°=2П радиан , мы попадаем в ту же точку ,

то угол 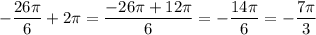   -\dfrac{26\pi }{6}+2\pi =\dfrac{-26\pi +12\pi }{6}=-\dfrac{14\pi }{6}=-\dfrac{7\pi }{3}    попадает в ту же

точку на единичной окружности , что и угол (-26П/6) .

Но угол (-7П/3)  не лежит между 0 и 2П . Поэтому надо прибавить не 2П,

а  больше , чтобы попасть в промежуток [ 0 ; 2П ] . Подбираем число n .

Если прибавить 3*2П , то получим  

-\dfrac{26\pi }{6}+3\cdot 2\pi =\dfrac{-26\pi +36\pi }{6}=\dfrac{10\pi }{6}=\dfrac{5\pi }{3}=300^\circ\ \ ,\ \ \ \ \dfrac{5\pi }{3}\in [\ 0\ ;\ 2\pi \ ]

Полученный угол  принадлежит промежутку [ 0; 2П ] .

Замечание.  Если прибавить 2*2П , то не получим угол из

промежутка [ 0;2П ] . Действительно,

-\dfrac{26\pi }{6}+2\cdot 2\pi =\dfrac{-26\pi +24\pi }{6}=\dfrac{-2\pi }{6}=-\dfrac{\pi }{3}  .

То есть можно сообразить, что в числитель к (-26П) надо прибавить число, большее 26П, чтобы получить положительный угол. И соответственно подбирать n .

Если прибавить 4*2П , то получим угол, который больше, чем 2П. Действительно,

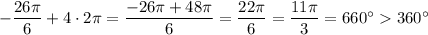
-\dfrac{26\pi }{6}+4\cdot 2\pi =\dfrac{-26\pi +48\pi }{6}=\dfrac{22\pi }{6}=\dfrac{11\pi }{3}=660^\circ 360^\circ

То есть n=2 и n=4 не подходит , а n=3 как раз подходит .

kirill23710
kirill23710
4,5(57 оценок)
Если число 6 умножить само на себя получится 36. или же (-6)

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS