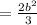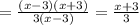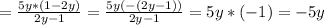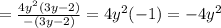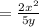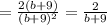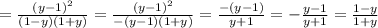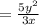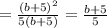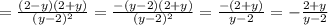Ответы на вопрос:
cos4x+1=1/2sin4x*(ctgx-tgx)
ctgx-tgx = cos2x/(sinx*cosx) - расписав ctg и tg через sin и cos , к общему знаменателю.
sin4x=2sin2x*cos2x - расписав по формуле синус суммы : sin(2x+2x)
1/2sin4x = 1/2 * 2sin2x*cos2x = cos2sx*sin2x
1/2sin4x*(ctgx-tgx)=cos2sx*sin2x* cos2x/(sinx*cosx) = 2cos^2(2x)
cos4x+1=2cos^2(2x) - формула понижение аргумента
2cos^2(2x) = 2cos^2(2x) -что и требовалось доказать!
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
11.4. Перерисуйте следующий граф так, чтобы его ребра не пе- ресекались:...
 Spez1821.11.2020 19:03
Spez1821.11.2020 19:03 -
Sin8°-sin10°-sin12°+sin14°/4sin11°cos1°sin²1°...
 nika0610200701.09.2020 14:00
nika0610200701.09.2020 14:00 -
Умоляююю запишіть арифметичну прогресію якщо : {а1+А2+А3=15 {а1•а2•а3=120...
 krit327.05.2020 14:10
krit327.05.2020 14:10 -
Функцію задано формулою y=1-x² , де -1...
 favorit1997127.07.2022 20:51
favorit1997127.07.2022 20:51 -
Здравствуйте с а) и в) Заранее...
 Ivanøva3414.04.2021 14:27
Ivanøva3414.04.2021 14:27 -
Упростите cosa-2sin3a-cos5a/cos5a-2cos3a-sina ...
 avadnure27.09.2020 16:46
avadnure27.09.2020 16:46 -
только 1,2,3,4 задание...
 volk007volk04.07.2022 07:46
volk007volk04.07.2022 07:46 -
Сума довжин двох суміжних сторін прямокутника дорівнює 23см а довжина...
 ленок20929.04.2022 20:31
ленок20929.04.2022 20:31 -
Розв яжіть рівняння х²+у²-8х+12у+51=0...
 lika77123.07.2020 05:05
lika77123.07.2020 05:05 -
на рисунку точка O-центр кола A і C -точки кола BD-дотична до до...
 Fluttys24.09.2022 02:40
Fluttys24.09.2022 02:40

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.