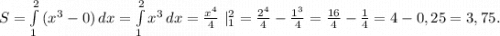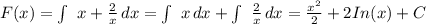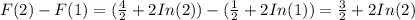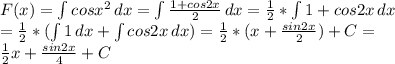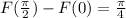Регистрация Спросить otvet5GPT
gfyfhh
31.01.2021 03:30
Алгебра
Есть ответ 👍

Обчислити площу фігури, обмеженої графіком функції f(x) = x ^ 3 , прямими x = 1 , x = 2 та віссю абсцис.

150
161
Посмотреть ответы 2

Ответы на вопрос:

mishakkkk
mishakkkk
4,5(51 оценок)

Объяснение:

f(x)=x³;  x=1;   x=2;  y=0.

S=\int\limits^2_1 {(x^3-0)} \, dx= \int\limits^2_1 {x^3} \, dx=\frac{x^4}{4}\ |^2_1=\frac{2^4}{4}-\frac{1^3}{4} =\frac{16}{4}-\frac{1}{4}=4-0,25=3,75.

ответ: S=3,75 кв. ед.

умный321
умный321
4,7(20 оценок)

a)

Действуем через нахождения первообразной, а затем вычитания пределов интегрирования:

F(x) = \int\ {x + \frac{2}{x} } \, dx = \int\ {x} \, dx + \int\ { \frac{2}{x} } \, dx = \frac{x^2}{2}+ 2In(x) + C

Вычитаем значения функции, чтобы получить итоговый ответ:

F(2) - F(1) = (\frac{4}{2} + 2In(2)) - (\frac{1}{2} + 2In(1)) = \frac{3}{2} + 2In(2)

б)

Действуем также как  в пункте а):

F(x) = \int{cos x^2} \, dx = \int{\frac{1 + cos 2x}{2} } \, dx = \frac{1}{2} * \int{1 + cos2x} \, dx \\ = \frac{1}{2} * ( \int{1} \, dx + \int{cos2x} \, dx) = \frac{1}{2} * (x + \frac{sin 2x}{2} ) + C = \\ \frac{1}{2} x + \frac{sin2x}{4} + C

Подставляем границы интегрирования в первообразную:

F(\frac{\pi }{2}) - F(0) = \frac{\pi }{4}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS