16.11.2022 10:54

Физика

Есть ответ 👍

Две длинные прямые параллельные нити, заряженные равномерно с линейной плотностью 20 нКл/м, находятся на расстоянии 10 см. Найти напряженность поля в точке, лежащей на расстоянии 10 см от обеих нитей. Две длинные прямые параллельные нити, заряженные равномерно с линейной плотностью 20 нКл/м, находятся на расстоянии 10 см. Найти напряженность поля в точке, лежащей на расстоянии 10 см от обеих нитей.

276

398

Посмотреть ответы 1

Ответы на вопрос:

ааааааспасите

Физика

4,6(81 оценок)

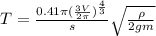
$T=\frac{0.41\pi (\frac{3V}{2\pi } )^{\frac{4}{3} }}{s}\sqrt{\frac{\rho}{2gm} }$

Объяснение:

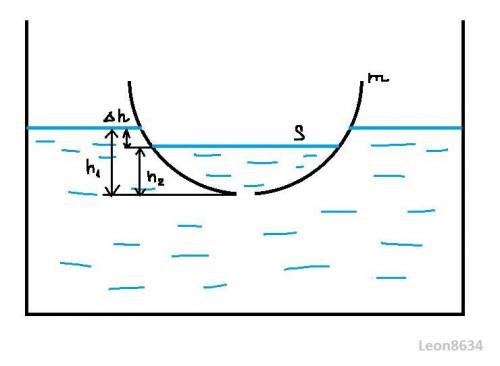
По мере погружения чаши создается перепад высот жидкости внутри и снаружи нее, этот перепад не позволяет ей утонуть мгновенно, выразим его пренебрегая толщиной стенок чаши

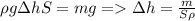$\rho g\Delta hS=mg = \Delta h=\frac{m}{S\rho}$ где S - площадь поверхности воды в чаше (в первом приближении).

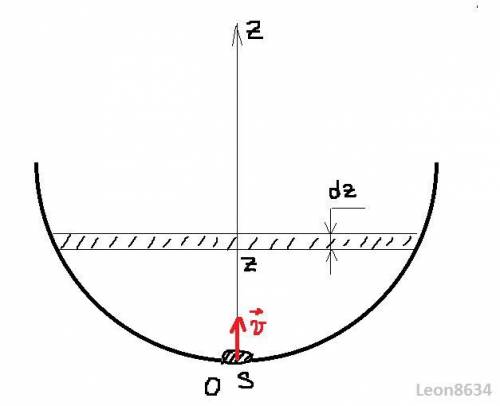
Пусть вода в чаше находится на уровне z и повысилась на малое dz, тогда из условия неразрывности потока можно записать

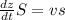
$\frac{dz}{dt}S=vs$

где S - площадь поверхности воды, а s - площадь отверстия.

Выразим площадь поверхности воды через z, для этого вспомним кое что из школы

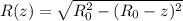
$R(z)=\sqrt{R_0^2-(R_0-z)^2}$

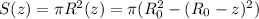
$S(z)=\pi R^2(z)=\pi (R^2_0-(R_0-z)^2)$

где R₀ - радиус чаши (можно найти из объема в конце)

Скорость втекания жидкости в отверстие найдем по формуле Торричелли

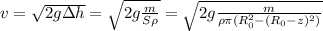
$v=\sqrt{2g\Delta h}=\sqrt{2g\frac{m}{S\rho} }=\sqrt{2g\frac{m}{\rho \pi (R_0^2-(R_0-z)^2)} }$

Подставляя все в дифференциальное уравнение получим

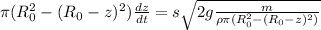
$\pi (R_0^2-(R_0-z)^2)\frac{dz}{dt}=s\sqrt{2g\frac{m}{\rho \pi (R_0^2-(R_0-z)^2)} }$

Несколько упростим

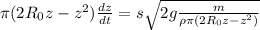
$\pi (2R_0z-z^2)\frac{dz}{dt}=s\sqrt{2g\frac{m}{\rho \pi (2R_0z-z^2)} }$

Попробуем разделить переменные

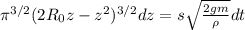
$\pi ^{3/2}(2R_0z-z^2)^{3/2}dz=s\sqrt{\frac{2gm}{\rho} } dt$

Проинтегрируем обе части

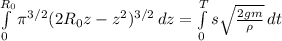
$\int\limits^{R_0}_0 {\pi ^{3/2}(2R_0z-z^2)^{3/2}} \, dz=\int\limits^T_0 {s\sqrt{\frac{2gm}{\rho} } \, dt$

Левый интеграл находим не без "костылей", правый берется легко

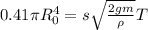
$0.41\pi R_0^4=s\sqrt{\frac{2gm}{\rho} }T$

Откуда время вытекания

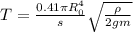
$T=\frac{0.41\pi R_0^4}{s} \sqrt{\frac{\rho}{2gm} }$

Осталось найти радиус, если объем чаши V объем всей сферы 2V отсюда

$\frac{4}{3}\pi R_0^3=2V = R_0=\sqrt[3]{\frac{3V}{2\pi } }$

Окончательно

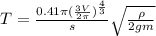$T=\frac{0.41\pi (\frac{3V}{2\pi } )^{\frac{4}{3} }}{s}\sqrt{\frac{\rho}{2gm} }$ .

Миску массой m и объёмом V имеющую дырку на днище площадью S помещают на воду . Через сколько времен

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Физика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.