В прямоугольном треугольнике гипотенуза равна 13см, а сумма катетов равна 17см. Найти катеты треугольника.

231

287

Посмотреть ответы 2

Ответы на вопрос:

Таня5463

Геометрия

4,6(25 оценок)

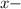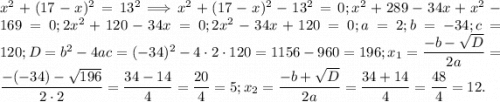
Пусть один катет, второй - (17-x). По теореме Пифагора: $x^{2} +(17-x)^2=13^2\Longrightarrow x^{2} +(17-x)^2-13^2=0; x^2+289-34x+x^{2} -169=0; 2x^2+120-34x=0; 2x^2-34x+120=0; a=2;b=-34;c=120;D=b^2-4ac=(-34)^2-4\cdot2\cdot120=1156-960=196; x_{1} =\dfrac{-b-\sqrt{D} }{2a} =\dfrac{-(-34)-\sqrt{196} }{2\cdot2} =\dfrac{34-14}{4} =\dfrac{20}{4} =5; x_{2} =\dfrac{-b+\sqrt{D} }{2a} =\dfrac{34+14}{4} =\dfrac{48}{4}=12.$

Сложим корни: 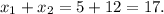$x_{1}+x_{2} =5+12=17.$ Так как сумма корней равна 17, то они являются катетами. ответ: катеты равны 5 и 12.

При решении квадратного уравнения применялась еще одна формула: 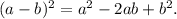(a-b)^2=a^2-2ab+b^2.

Oremi

Геометрия

4,5(47 оценок)

Если треугольник abc, в котором угол а=60⁰, сторона ав в два раза больше стороны ас, то этот треугольник прямоугольный (это легко доказывается по теореме косинусов).а так как в окружность радиуса 4 вписан прямоугольный треугольник abc,то гипотенуза ав равна 2r, а сторона ас равна радиусу r и равна 4. биссектриса ам делит угол а пополам.треугольник амс - прямоугольный с углом мас 30°. тогда отрезок мс = ас*tg30° = 4/√3.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.