Математика: Найти все комплексные числа , сопряжённые своему кубу?

mrkrbnv

15.03.2022 18:03

Математика

Есть ответ 👍

Найти все комплексные числа , сопряжённые своему кубу?

127

366

Посмотреть ответы 3

Ответы на вопрос:

мария22228

Математика

4,6(81 оценок)

0, 1, -1, i, -i.

Пошаговое объяснение:

Для числа a+bi сопряженное a-bi. Получаем (a+bi)^3 = a-bi;

a^3 + 3 a^2 bi + 3 a (bi)^2 + (bi)^3 = a - bi

a^3 + 3 a^2 bi - 3 a b^2 - b^3 i = a - bi

Действительные и мнимые части должны совпадать:

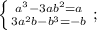$\left \{ {{a^3-3ab^2=a} \atop {3a^2b-b^3=-b}} \right. ;$ если a и b не равны 0, то

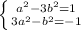
$\left \{ {{a^2-3b^2=1} \atop {3a^2-b^2=-1}} \right.$

Складываем уравнения: 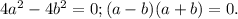4a^2-4b^2=0; (a-b)(a+b) = 0. Отсюда a=b или a = -b. В любом из этих случаев из первого уравнения a^2-3a^2=1; -2a^2 = 1 , что невозможно.

Если a=0, то из второго уравнения (до сокращения) 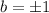$b=\pm1$ или b = 0.

Если b=0, то из первого уравнения $a=\pm1$ или a = 0.

Итого 5 чисел: 0, 1, -1, i, -i.

Jack1703

Математика

4,7(79 оценок)

ответ:x =i

Пошаговое объяснение: Пусть число z=x + iy

– искомое комплексное число, где x и y – действительные числа. Тогда число z⁻= x - iy , сопряженное числу z

По условию задачи имеем:z⁻ = z³ , ⇒ (x+iy)³= x - iy ⇒

x³+3x²iy+3xi²y²+i³y³= x - iy

Преобразовав это уравнение, получим: (x³+3x²y)+ i(3x²y-y³)= x-iy

У нас два комплексных числа равны , значит будут равны соответственно их действительные и мнимые части:

x³+3x²y=х и 3x²y-y³= -у

Возможны два случая: 1) если у≠0, то

x³+3xy²=х и 3x²-y²= -1

у² =1+3х² ⇒

х³+3х(1+3х²)=х ⇒ 10х³ + 2х=0 ⇒ 2х(5х²+1) = 0 ⇒ х =0, тогда у=1+3·0²=1 Этот случай имеет следующее решение: (0; 1)

Тогда число z₁=0+1·i = i ⇒ z₁= i искомое комплексное число

2) если у=0, то

х³ - х =0 и у = 0

х(х² -1) =0

х=0 или х=±1

Этот случай имеет следующие решения: (0; 0) и (1; 0), (-1; 0)

тогда им соответствуют числа

z₂=0+0·i = 0 ( действительное число)

z₃= 1+0·i = 1 ( действительное число)

z₄=-1+0i= -1 ( действительное число)

Значит х = i -искомое комплексное число

GDIZzzEr

Математика

4,6(31 оценок)

11*8=88(см²) площадь прямоугольника 5*5=25(см²) площадь одного квадрата 25*2=50(см²) площадь двух квадратов 88-50=38(см²) площадь оставшейся фигуры

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.