Регистрация Спросить otvet5GPT
nysha046
13.09.2020 19:49
Геометрия
Есть ответ 👍

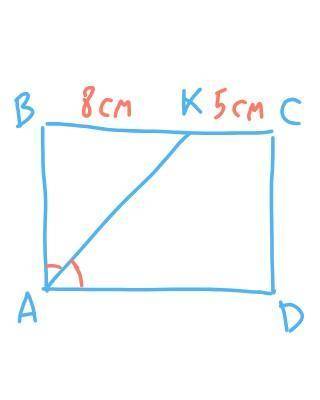
Бісектриса кута А прямокутника АВСД ділить сторону ВС на відрізки 8 і 5 см починаючи від вершини В. Знайти периметр прямокутника

199
368
Посмотреть ответы 2

Ответы на вопрос:

Алёнка12082004
Алёнка12082004
4,4(77 оценок)

Периметр прямоугольника равен удвоенной сумме двух его смежных сторон. P = 2(AB+BC),

BC = BK + KC = 8 см + 5 см = 13 см.

AK — биссектрисса угла A, угол BAK = угол KAD = 90°÷2 = 45°,

Рассмотрим треугольник ABK. Сумма углов треугольника равна 180°. угол BKA = 180° – угол ABK – угол BAK = 180° – 90° – 45° = 45°, угол BKA = угол BAK, углы при основании равны, треугольник — равнобедренный, значит боковые стороны равны, AB = BK = 8см.

P = 2(AB + BC) = 2(8см + 13см) = 2 × 21 см = 42 см.

ответ: 42 см


Бісектриса кута А прямокутника АВСД ділить сторону ВС на відрізки 8 і 5 см починаючи від вершини В.
Бісектриса кута А прямокутника АВСД ділить сторону ВС на відрізки 8 і 5 см починаючи від вершини В.
гуманитарий0013
гуманитарий0013
4,5(45 оценок)
Построим высоту сн к стороне ав.  в прямоугольном треугольнике свн угол в = 45 градусов (по условию), тогда угол всн = 90 - 45 = 45 градусов => треугольник равнобедренный, вн = сн. известно, что  вс = 6,  пусть ан = вн =  х,  тогда по теореме пифагора вс^2 = вн^2 + сн^2 36 = х^2 + x^2;   36 = 2x^2; x^2 = 18; х = корень из 18;   треугольник анс - прямоугольный.  угол а = 60 градусов (по условию), тогда  угол нса = 90 - 60 = 30 градусов. пусть ас = 2х, тогда ан = х (так как катет, лежащий против угла, равного 30 градусов, равен 1/2 гипотенузы). по теореме пифагора ас^2 = ан^2 + нс^2 4х^2 = 18  + х^2;   4х^2 -  х^2 = 18; 3х^2  = 18; х^2  = 6; х = корень из 6;   тогда ас = 2х = 2 корня из 6 ответ: 2  корня из 6

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS