rsdgdddddddddddd

07.01.2022 14:12

Есть ответ 👍

Биссектрисы треугольника ABC пересекаются в точке О, причем угол AOB = угол ВОС = 110°. а) Докажите, что треуголь- ник ABC равнобедренный, и укажите его основание.
б) Найдите углы данного треугольника.
С РИСУНКОМ

245

491

Посмотреть ответы 2

Ответы на вопрос:

mimra23213

Геометрия

4,4(7 оценок)

Объяснение:

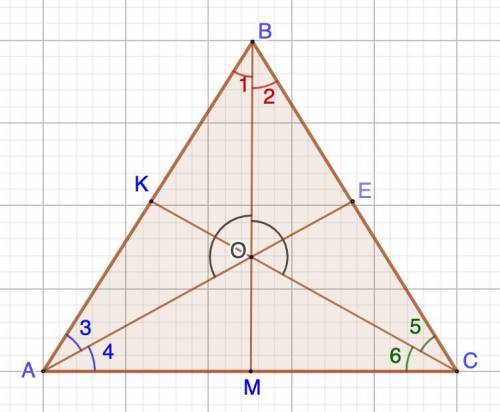
Дано: ΔАВС

АЕ, ВМ, СК - биссектрисы;

∠AOB = ∠ ВОС = 110°.

а) Доказать: ΔАВС - равнобедренный;

б) Найти: ∠А; ∠В; ∠С.

а) Доказательство:

Рассмотрим ΔАОВ и ΔВОС.

∠1=∠2 (условие)

∠AOB = ∠ ВОС (условие)

ВО - общая

⇒ ΔАОВ = ΔВОС (по 2 признаку)

⇒ АВ=ВС (как соответственные элементы)

⇒ ΔАВС - равнобедренный.

б) Решение:

1) ΔАОВ = ΔВОС ⇒АО=ОС (как соответственные элементы)

2) Рассмотрим ΔАОС (равнобедренный, п.1)

⇒ ∠4=∠6 (углы при основании равнобедренного треугольника равны)

∠АОС=360°-(∠AOB + ∠ ВОС)=360°-(110°+110°)=140°

Сумма углов треугольника равна 180°.

⇒ ∠4=∠6=(180°-140°):2=20°

3) ∠3=∠4 (условие)

⇒∠А=∠3+∠4=20°+20°=40°

4) ∠А=∠С=40° (при основании равнобедренного ΔАВС)

∠В=180°-(40°+40°)=100°

Faleck

Геометрия

4,8(33 оценок)

Косинус √3/2 , √2/2 , 1/2 синус 1/2 ,√2/2 , √3/2 тангенс √3/3 , 1 , √3

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.