Регистрация Спросить otvet5GPT
ayvazova2010
21.10.2020 10:24
Математика
Есть ответ 👍

Вычислить предел lim (d(n)/n) - где d(n), кол-во цифр числа n
n->+беск

215
377
Посмотреть ответы 2

Ответы на вопрос:

масяня194
масяня194
4,6(72 оценок)

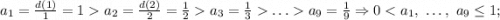
 a_1=\frac{d(1)}{1}=1 a_2=\frac{d(2)}{2}=\frac{1}{2}a_3=\frac{1}{3}\ldots a_9=\frac{1}{9}\Rightarrow 0

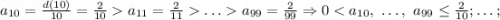
a_{10}=\frac{d(10)}{10}=\frac{2}{10}a_{11}=\frac{2}{11}\ldots a_{99}=\frac{2}{99}\Rightarrow 0

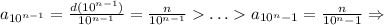
a_{10^{n-1}}=\frac{d(10^{n-1})}{10^{n-1}}=\frac{n}{10^{n-1}}\ldots a_{10^n-1}=\frac{n}{10^n-1}\Rightarrow

0

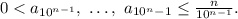
Последовательность 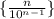\{\frac{n}{10^{n-1}}\} стремится к нулю, поэтому исходная последовательность стремится к нулю по лемме о "двух правоохранителях" (милиционерах, полицейских, жандармах, копах и т.д - в зависимости от страны и эпохи).

Доказать, что 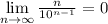\lim\limits_{n\to \infty}\frac{n}{10^{n-1}}=0 можно многими (с правила Лопиталя, теоремы Штольца, бинома Ньютона, неравенства Бернулли - кто подскажет еще ?).

Например,  бином Ньютона дает нам следующую оценку:

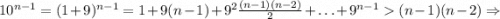
10^{n-1}=(1+9)^{n-1}=1+9(n-1)+9^2\frac{(n-1)(n-2)}{2}+\ldots +9^{n-1}(n-1)(n-2)\Rightarrow

0.

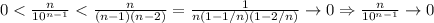Неравенство Бернулли применяем так:

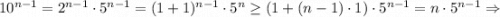
10^{n-1}=2^{n-1}\cdot 5^{n-1}=(1+1)^{n-1}\cdot 5^n\ge (1+(n-1)\cdot 1)\cdot 5^{n-1}=n\cdot 5^{n-1}\Rightarrow

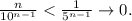
\frac{n}{10^{n-1}}

Лопиталь заменяет n на  x, проверяет наличие неопределенности

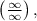\left(\frac{\infty}{\infty}\right), вычисляет предел отношения производных:

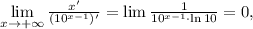\lim\limits_{x\to+\infty}\frac{x'}{(10^{x-1})'}=\lim\frac{1}{10^{x-1}\cdot \ln 10}=0, и поскольку предел отношения производных существует и равен нулю, исходный предел также равен нулю.

Штольц не так хорошо известен, но наш предел вычисляет мгновенно. Однако я устал и (возможно) утомил читателя. Поэтому, памятуя Козьму Пруткова, заканчиваю.

ЧакН0рис
ЧакН0рис
4,6(22 оценок)
Разкрываем скобки 10х - 6 = 6х - 14 неизвестные переносим влево, известные - вправо. меням, где нужно, знаки 10х - 6х = 6 - 14 считаем 4х = -8 х = -8 : 4 х = -2

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS