Математика: Найти производную второго порядка: y = e^x/2 sin2x

kamilla202

18.02.2020 16:19

Математика

Есть ответ 👍

Найти производную второго порядка:

y = e^x/2 sin2x

243

446

Посмотреть ответы 2

Ответы на вопрос:

Cennet55

Математика

4,6(9 оценок)

Пошаговое объяснение:

используются табличные производные и формулы

(uv)' = u'v + uv'

f(g(x))' = f'(g(x)) * g'(x)

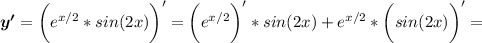
$\displaystyle \boldsymbol {y'}=\bigg (e^{x/2}*sin(2x)\bigg )'=\bigg (e^{x/2}\bigg )'*sin(2x)+e^{x/2}*\bigg (sin(2x)\bigg )'=$

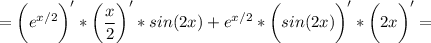
$\displaystyle =\bigg (e^{x/2}\bigg)'*\bigg (\frac{x}{2} \bigg )'*sin(2x)+e^{x/2}*\bigg (sin(2x)\bigg )'*\bigg (2x \bigg )'=$

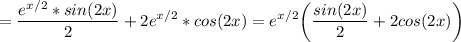
$\displaystyle =\frac{e^{x/2}*sin(2x)}{2} +2e^{x/2}*cos(2x)= e^{x/2}\bigg (\frac{sin(2x)}{2} +2cos(2x)\bigg )$

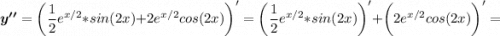
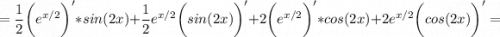
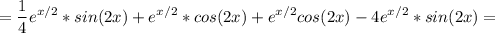
$\displaystyle \boldsymbol {y''} = \bigg (\frac{1}{2} e^{x/2}*sin(2x)+2e^{x/2}cos(2x)\bigg )'=\bigg (\frac{1}{2} e^{x/2}*sin(2x)\bigg )'+\bigg (2e^{x/2}cos(2x)\bigg )'=$ $\displaystyle =\frac{1}{2} \bigg(e^{x/2}\bigg )'*sin(2x)+\frac{1}{2} e^{x/2}\bigg (sin(2x)\bigg )'+2\bigg (e^{x/2}\bigg )'*cos(2x)+2e^{x/2}\bigg (cos(2x)\bigg )'=$ $\displaystyle =\frac{1}{4} e^{x/2}*sin(2x)+e^{x/2}*cos(2x)+e^{x/2}cos(2x)-4e^{x/2}*sin(2x)=$

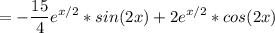
$\displaystyle =-\frac{15}{4} e^{x/2}*sin(2x) +2e^{x/2}*cos(2x)$

Маша4гклаша

Математика

4,5(28 оценок)

1) 3/8-1/6 = 9/24-4/24=5/24 (часть) пути прошел за вторые сутки

2) 3/8+5/24=9/24+5/24=14/24=7/12 (часть) - прошел за двое суток

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.