hatikomurka

01.06.2020 00:49

Геометрия

Есть ответ 👍

.Нужно найти площадь вписанного круга в прямоугольном треугольнике

184

398

Посмотреть ответы 3

Ответы на вопрос:

GoldFish1701

Геометрия

4,7(71 оценок)

В прямоугольный ΔАВС, ∠С=90 вписан круг .Биссектриса ∠А делит катет в отношении CD:DB=3:5. Найдите площадь круга

Решение Площадь круга S= πr² .Радиус вписанной окружности найдем из формулы S=1/2*P*r .

1) Тк " биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника" , то CD:СА=ВD:АВ или 3:СА=5:АВ ⇒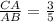 $\frac{CA}{AB} =\frac{3}{5}$ , а это по определению sinB .

2) По основному тригонометрическому тождеству

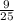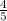
sin²B+cos²B=1 получаем cosB=√(1- $\frac{9}{25}$ )= $\frac{4}{5}$

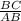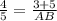3) cosB= $\frac{BC}{AB}$ или $\frac{4}{5} =\frac{3+5}{AB}$ ⇒ AB=10.

По т Пифагора АС=√(АВ²-ВС²)=√(100-64)=6

4) S=1/2*P*r

1/2*BC*AC=1/2*(AB+BC+AC)*r

1/2*8*6=1/2*24*r ⇒ r=2 ед

S(круга)=π*2²=4π (ед²)

alenushkabelya

Геометрия

4,5(3 оценок)

AC/AB =CD/DB =3/5 (т о биссектрисе)

AC=3x, AB=5x

BC =√(AB^2-AC^2) =4x =8 => x=2

r =(AC+BC-AB)/2 =x =2

S=пr^2 =4п

Отрезки касательных из одной точки равны: CK=CN итд

в любом треугольнике CK=p-AB

в прямоугольном треугольнике CKIN - квадрат => r =CK

.Нужно найти площадь вписанного круга в прямоугольном треугольнике

tusovki

Геометрия

4,4(61 оценок)

N-количество углов (n-2)•180

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.