Регистрация Спросить otvet5GPT
SlavaKirja
11.03.2020 07:31
Геометрия
Есть ответ 👍

Найти периметр параллелограмма объясните как найти эти две стороны
​

189
350
Посмотреть ответы 1

Ответы на вопрос:

margogalaxowa
margogalaxowa
4,7(25 оценок)

32 cм²

Объяснение:

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему:

Sбок= 1/2*(Р1+Р2)*L,

где Р1 и Р2 - периметры оснований пирамиды, L - апофема (высота боковой грани правильной усеченной пирамиды)

Найдём сто­роны оснований правильной четырехугольной усеченной пирамиды.

Диагональ квадрата: d = a√2, где а  - сторона квадрата.

⇒ а = d/√2

АД = 6/√2 = 3√2, А1Д1= 2/√2 = √2.

Р1=4*АД= 4 * 3√2 = 12√2 см - периметр верхнего основания.

Р2=4*А1Д1=4√2 см - периметр нижнего основания пирамиды.

Найдем апофему L

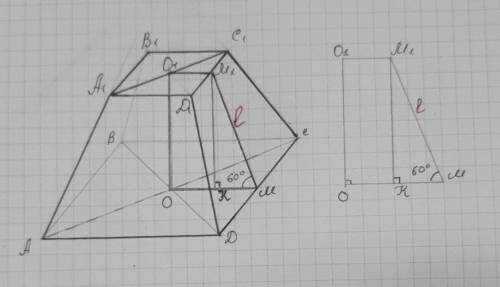
Основания усеченной пирамиды - квадраты. Проведем из центров оснований перпендикуляры ОМ⊥ДС и О1М1⊥Д1С1. ОМ и О1М1 - радиусы вписанных окружностей в основания.

Т.к. r=a /2 (половина стороны основания), то  

О1М1= А1Д1/2 = 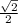 \frac{\sqrt{2} }{2}

ОМ = АД/2 = 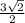  \frac{3\sqrt{2} }{2}

Опустим перпендикуляр М1К из точки М1 верхнего основания  на нижнее основание. Получим прямоугольный ΔМ1КМ.

Т.к. М1К⊥КМ, КМ⊥ДС,  то М1М⊥ДС ( по теореме о трёх перпендикулярах) ⇒∠М1МК = 60° (это данный нам линейный угол двугранного угла при ребре большего основания).

КМ = разнице расстояний от центров оснований до боковых сторон, то есть КМ = ОМ-О1М1= 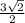  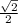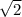\frac{3\sqrt{2} }{2} - \frac{\sqrt{2} }{2} = \sqrt{2} см.

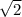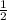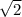Тогда гипотенуза (апофема) L = ММ1 = КМ / cos 60° = \sqrt{2} : \frac{1}{2} = 2\sqrt{2} cм

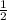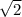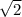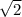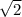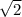Sбок = \frac{1}{2} * ( 12\sqrt{2} + 4\sqrt{2} ) * 2\sqrt{2} = \sqrt{2} (12+4) \sqrt{2} = 2*16=32 cм²


диагонали основ правильной четырехугольной усеченной пирамиды равны 6 и 2 см, а двугранный угол при

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS