Регистрация Спросить otvet5GPT
Wertik3
25.11.2022 05:35
Алгебра
Есть ответ 👍

РЕШИТЬ ЭТО ЗАДАНИЕ , ответ 5 ​

236
375
Посмотреть ответы 2

Ответы на вопрос:

mivliev38p08iax
mivliev38p08iax
4,4(50 оценок)

sin2x-(\sqrt2+1)(sinx+cosx)+\sqrt2+1=0\ \ ,\ \ x\in [-6\ ;\ 6\ ]2sinx\cdot cosx-(\sqrt2+1)(sinx+cosx)+\sqrt2+1=0Zamena:\ \ t=sinx+cosx\ ,t^2=(sinx+cosx)^2=\underbrace{sin^2x+cos^2x}_{1}+2sinx\cdot cosx=1+2sinx\cdot cosx\ \ ,2sinx\cdot cosx=t^2-1\ \ \Rightarrow \ \ \ sinx\cdot cosx=\dfrac{t^2-1}{2}t^2-1-(\sqrt2+1)\cdot t+\sqrt2+1=0\ ,t^2-(\sqrt2+1)\cdot t+\sqrt2=0\ \ ,D=(\sqrt2+1)^2-4\cdot \sqrt2=(2+2\sqrt2+1)-4\sqrt2=2-2\sqrt2+1=(\sqrt2-1)^2

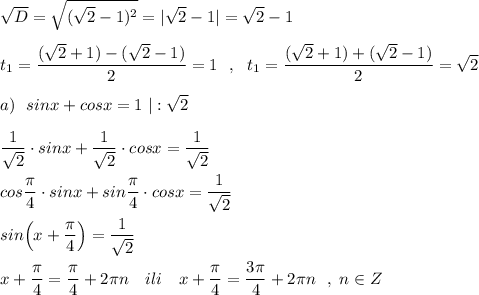
\sqrt{D}=\sqrt{(\sqrt2-1)^2}=|\sqrt2-1|=\sqrt2-1t_1=\dfrac{(\sqrt2+1)-(\sqrt2-1)}{2}=1\ \ ,\ \ t_1=\dfrac{(\sqrt2+1)+(\sqrt2-1)}{2}=\sqrt2a)\ \ sinx+cosx=1\ |:\sqrt2dfrac{1}{\sqrt2}\cdot sinx+\dfrac{1}{\sqrt2}\cdot cosx=\dfrac{1}{\sqrt2}cos\dfrac{\pi}{4}\cdot sinx+sin\dfrac{\pi }{4}\cdot cosx=\dfrac{1}{\sqrt2}sin\Big(x+\dfrac{\pi}{4}\Big)=\dfrac{1}{\sqrt2}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+2\pi n\ \ \ ili\ \ \ x+\dfrac{\pi}{4}=\dfrac{3\pi}{4}+2\pi n\ \ ,\ n\in Z

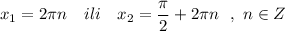
x_1=2\pi n\ \ \ ili\ \ \ x_2=\dfrac{\pi}{2}+2\pi n\ \ ,\ n\in Z

x_1\in [-6\ ;\ 6\ ]:\ \ 6\ rad\approx 344^\circ \ \ ,\ \ x_1\in [-344^\circ \ ;\ 344^\circ ]x_1=360^\circ \cdot n\ \ ,n=0\ \ \to \ \ x_1=0\in [-6;6\ ] \ x_2=\dfrac{\pi }{2}+2\pi n=90^\circ +360^\circ n\ ,n=-1\ \ \to \ \ x_2=-270^\circ=-\dfrac{3\pi}{2}\in [-6;6\ ]n=0\ \ \to \ \ x_2=90^\circ =\dfrac{\pi}{2}\in [-6;6\ ]

При других значениях  n  корни не будут входить в указанный промежуток .

b)\ \ sinx+cosx=\sqrt2\ |:\sqrt2dfrac{1}{\sqrt2}\cdot sinx+\dfrac{1}{\sqrt2}\cdot cosx =1sin\Big(x+\dfrac{\pi}{4}\Big)=1\ \ \ \Rightarrow \ \ \ x+\dfrac{\pi}{4}=\dfrac{\pi}{2}+2\pi k\ \ ,\ \ x=\dfrac{\pi}{4}+2\pi k\ ,\ k\in Zx=45^\circ +360^\circ kk=-1\ \ \to \ \ x=-315^\circ =-\dfrac{7\pi}{4}\in [-6;6\ ]k=0\ \ \to \ \ x=45^\circ =\dfrac{\pi}{4}\in [-6;6\ ]

При других значениях  k  корни не будут входить в указанный промежуток .

Otvet:\ 1)\ x_1=2\pi n\ ,\ x_2=\dfrac{\pi}{2}+2\pi n\ ,\ x_3=\dfrac{\pi}{4}+2\pi k\ \ ,\ \ n,k\in Z\ ;{}\ \ \ 2)\ \ x\in [-6;6\ ]\ \ \Rightarrow \ \ x=0\ ;\ -\dfrac{7\pi}{4}\ ;\ -\dfrac{3\pi}{2}\ ;\ \dfrac{\pi}{4}\ ,\ \dfrac{\pi}{2}\ ;\ \ vsego\ 5 \ kornej\ .

dradya
dradya
4,7(32 оценок)

ответ:  площадь треугольника равна 54

Объяснение:

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS