Регистрация Спросить otvet5GPT
ghj42
18.06.2023 05:35
Алгебра
Есть ответ 👍

1.75. Представьте выражение в виде степени с основанием x: 1) (х^2)^5 : (х^3)^2;
2) (х^3)^4 : (х^2)^5;
3) (х^3 : х^2)^5;
4) (х^4 / х) ^3;

126
194
Посмотреть ответы 2

Ответы на вопрос:

bulochka228
bulochka228
4,7(83 оценок)

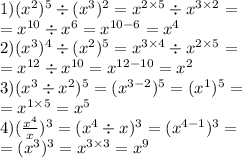
1)(x {}^{2} ) {}^{5} \div (x {}^{3} ) {}^{2} = x {}^{2 \times 5} \div x {}^{3 \times 2} = \\ = x {}^{10} \div x {}^{6} = x {}^{10 - 6} = x {}^{4} \\ 2)(x {}^{3} ) {}^{4} \div (x {}^{2} ) {}^{5} = x {}^{3 \times 4} \div x {}^{2 \times 5} = \\ = x {}^{12} \div x {}^{10} = x {}^{12 - 10} = x {}^{2} \\ 3)(x {}^{3} \div x {}^{2} ) {}^{5} = (x {}^{3 - 2} ) {}^{5} = (x {}^{1} ) {}^{5} = \\ = x {}^{1 \times 5} = x {}^{5} \\ 4)( \frac{x {}^{4} }{x} ) {}^{3} = (x {}^{4} \div x {}^{} ) {}^{3} = (x {}^{4 - 1}) {}^{3} = \\ = (x {}^{3} ) {}^{3} = x {}^{3 \times 3} = x {}^{9}

При умножении чисел с одинаковыми основаниями их степени складываются, при делении вычитаются, если степень возводится в степень, то эти степени умножаются

lfybk2001zp099tv
lfybk2001zp099tv
4,6(70 оценок)

доказальство методом индукции.

база индукции n=1 : а значит число выражение 7 * 5 ^ 2n + 12 * 6 ^ n при n=1 делится на 19

 

гипотеза индукции. пусть при n=k выражение 7 * 5 ^ (2n) + 12 * 6 ^ n делится на 19, т.е. выражение 7 * 5 ^ (2k) + 12 * 6 ^ k делится на 19

инукционный переход. докажем, что тогда при n=k+1 выражение 7 * 5 ^ (2n) + 12 * 6 ^ n делится на 19

, что делится на 19 , так какждый из слагаемых делится на 19 (во второй как в произведение входит множитель 19, в первое слагамое как в произведение по гипотезе индукции входит множитель, который делится на 19)

по принципу индукции при любом целом неотрицательном n выражение 7 * 5 ^ 2n + 12 * 6 ^ n делится на 19

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS