gasuslov

25.05.2022 00:26

Алгебра

Есть ответ 👍

, я , не могу решить эти задания

228

245

Посмотреть ответы 2

Ответы на вопрос:

Андрюша1789

Алгебра

4,6(1 оценок)

$\dfrac{x-5}{2x + 1} \leqslant 0$

2x ≠ -1 ⇒ x ≠ -0.5

x -5 = 0 ⇒ x = 5

Метод интервалов

+ - +

(- 0,5) [5]

x ∈ (-0.5; 5]

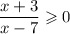
$\dfrac{x+3}{x - 7} \geqslant 0$

х ≠ 7

х + 3 = 0 ⇒ х = -3

Метод интервалов

+ - +

[- 3] (7)

x ∈ (-∞; -3]∪ (7; +∞)

-x² - 5x + 6 ≤ 0

-x² - 5x + 6 = 0

D = 25 +24 = 49 = 7²

x₁ = -0.5 · (5 - 7) = 1

x₂ = -0.5 · (5 + 7) = -6

Метод интервалов

- + -

[- 6] [1]

x ∈ (-∞; -6] ∪ [1; + ∞)

3x² - 8x - 3 ≥ 0

3x² - 8x - 3 = 0

D = 64 +36 = 100 = 10²

x₁ = (8 - 10) : 6 = -1/3

x₂ = (8 + 10) : 6 = 3

Метод интервалов

+ - +

[- 1/3] [3]

x ∈ (-∞; -1/3] ∪ [3; + ∞)

daffidovа

Алгебра

4,6(18 оценок)

$cosx-\sqrt{3}sinx=\sqrt{2} |: {1}{2}cosx-\frac{\sqrt{3} }{2}sinx=\frac{\sqrt{2} }{2}{\pi }{3}cosx-sin\frac{\pi }{3}sinx=\frac{\sqrt{2} }{2}(\frac{\pi }{3}+x)=\frac{\sqrt{2} }{2}{\pi }{3}+x=\pm arccos\frac{\sqrt{2} }{2}+2\pi n,n\in {\pi }{3}+x=\pm \frac{\pi }{4}+2\pi n,n\in =\pm\frac{\pi }{4}-\frac{\pi }{3}+2\pi n,n\in {1}=\frac{\pi }{4}-\frac{\pi }{3}+2\pi n=-\frac{\pi }{12}+2\pi n,n\in z$

$x_{2}=-\frac{\pi }{4}-\frac{\pi }{3}+2\pi n,n\in {2}=-\frac{7\pi }{12}+2\pi n,n\in z$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.