Найдите какую-нибудь пару натуральных чисел, которая являет- ся решением уравнения

251

322

Посмотреть ответы 2

Ответы на вопрос:

denbulking

Алгебра

4,7(97 оценок)

Найти по одному решению каждого уравнения - не проблема. А вот найти все натуральные решения - это намного более сложная задача.

Простейшие решения в первой задаче (1;1)), во второй (3;2), в третьей (1;1). Дальше можете не смотреть (а можете посмотреть).

1) Преобразуем так: (x²-1)(y²-1)=0; x²-1=0 или y²-1=0; x=1 или y=1.

То есть решения такие: (1;1), (1;2), (1;3), ..., (2;1), (3;1),...

2) Преобразуем так: x²-2y²=1. Это намного более сложная задача - частный случай так называемого уравнения Пелля. Заинтересуетесь - почитайте литературу на эту тему, только сначала попробуйте решить сами. Годится, как я уже писал, пара (3;2), остальные пары получаются из этой по такому правилу: если была пара (x;y), то следующая равна (3x+4y;2x+3y). Поэтому получаем второе решение (3·3+4·2;2·3+3·2)=(17;12). Можете построить сколько угодно решений по такому правилу.

3) Конечно, если m=n, то 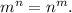m^n=n^m. Поэтому мы уже имеем бесконечное множество решений. Но ими множество решений не исчерпывается. По крайней мере 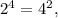2^4=4^2, то есть получили решения (2;4) и (4;2). Докажем, что других решений нет. Преобразуем так: $\sqrt[m]{m}=\sqrt[n]{n}.$

Рассмотрим функцию 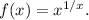$f(x)=x^{1/x}.$ (x≥1)

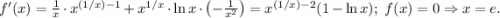
$f'(x)=\frac{1}{x}\cdot x^{(1/x)-1}+x^{1/x}\cdot \ln x\cdot \left(-\frac{1}{x^2}\right)= x^{(1/x)-2}(1-\ln x);\ f(x)=0\Rightarrow x=e.$

Слева от e производная положительна, справа отрицательна, то есть слева от e функция возрастает, справа убывает.

$f(1)=1\sqrt[5]{5}\ldots,$ при этом все эти числа кроме f(1) больше 1. Поэтому кроме f(2)=f(4) все эти числа разные.

ответ в третьей задаче: (2;4), (4;2), (1;1), (2;2), (3;3),...

прощения, если не все было понятно - в будущем разберетесь))

RomanenkoAA

Алгебра

4,5(80 оценок)

1) раскладываем по степеням в порядке убывания: x^2-14x+49 2) извлекаем квадрат из крайних членов - получается, что это x и 7. 3) проверяем удвоенное произведения членов: 2*7*x = 14x - всё правильно. 4) смело пишем: (x-7)^2 (внутри минус, т.к. перед 14x тоже минут). всё. з.ы. советую повторить формулы сокращенного умножения)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.