Регистрация Спросить otvet5GPT
талифа4
06.05.2023 14:14
Алгебра
Есть ответ 👍

Решите уравнение 5+7y-12/3 =y+13.
в ответе должно быть 9(написано в конце книги)​

269
350
Посмотреть ответы 1

Ответы на вопрос:

alexcozearschi
alexcozearschi
4,5(86 оценок)

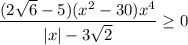
\displaystyle \frac{(2\sqrt6 - 5)(x^2-30)x^4}{|x|-3\sqrt2} \geq 0

Найдём ОДЗ:

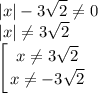
\displaystyle |x|-3\sqrt2\ne 0\\ |x|\ne 3\sqrt 2\\\left [{ {{x\ne 3\sqrt 2} \atop {x\ne -3\sqrt 2}} \right.

В числителе есть скобка, от которой можно избавиться 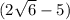(2\sqrt6-5).

Узнаем знак, относительно 0, этой скобки.

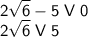
\sf\displaystyle 2\sqrt 6-5\;V\; 0\\ 2\sqrt 6 \; V\; 5

Возведём во вторую степень обе стороны. Эти стороны положительны.

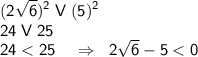
\displaystyle \sf (2\sqrt6)^2 \; V \; (5)^2\\24 \; V \; 25\\ 24<25 \;\;\;\; \Rightarrow \;\; 2\sqrt 6 -5<0

Поделим наше неравенство на 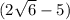(2\sqrt6-5), поменяв знак нашего неравенства на противоположный.

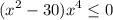
\displaystyle (x^2-30)x^4\leq 0

Найдём нули.

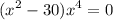
\displaystyle (x^2-30)x^4=0

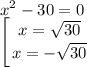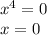
\displaystyle x^2-30=0\\\left [{ {{x=\sqrt{30}} \atop {x=-\sqrt{30}}} \right. или x^4=0\\x=0

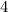4 чётная степень, знак, проходящий через 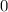0, не меняется.

Воспользуемся методом интервалов.

++++++ \Big[-\sqrt{30}\Big]---\Big[0\Big] --- \Big [ \sqrt{30}\Big] ++++++x

Узнаем, где находятся наши ограничения, прежде чем нанесём их на нашу прямую.

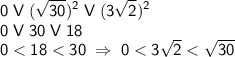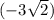\displaystyle \sf 0 \; V\; (\sqrt{30})^2 \; V\; (3\sqrt 2)^2\\ 0 \; V\; 30\; V \; 18 \\ 0<18<30 \;\Rightarrow \;0<3\sqrt2< \sqrt{30} - с (-3\sqrt2) произойдёт всё симметрично 0.

+\Big[-\sqrt{30}\Big ]---\Big(-3\sqrt2\Big)---\Big[0\Big]---\Big(3\sqrt2\Big)---\Big[\sqrt{30}\Big]+x

ответ: \displaystyle x\in\Big [-\sqrt{30};-3\sqrt2\Big)\cup\Big(-3\sqrt2;3\sqrt2\Big)\cup\Big(3\sqrt2; \sqrt{30}\Big]

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS