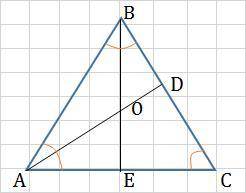
В равносторонние треугольнике ABC биссектрисы AD и BE пересекаются в точке O. Найдите угол AOE между биссектриса и треугольника ABC

224

239

Посмотреть ответы 2

Ответы на вопрос:

KrutoiYurka2008

Геометрия

4,5(18 оценок)

Объяснение:

1) В равностороннем треугольнике все углы равны между собой и = 60°

2) Биссектриса в равностороннем треугольнике является также его медианой и высотой, поэтому ВЕ ⊥ АС и, следовательно, ∠ВЕА = 90°

3) Рассмотрим ΔАОЕ.

∠ВЕА = 90°

∠ОАЕ = 60°/2 = 30° (т.к. АD - биссектриса ∠А и , значит, делит этот угол пополам)

Теорема: Сумма всех углов треугольника равна 180º,т.е.

∠ВЕА + ∠ ОАЕ + ∠АОЕ = 180°

90° + 30° + ∠АОЕ = 180°, откда

∠АОЕ = 180° - 120° = 60°

viktoriabuble

Геометрия

4,5(75 оценок)

Рассмотрим ΔАВС с прямым ∠С; ∠А=60°. АВ - гипотенуза, АС и СВ - катеты.

1) Треугольник прямоугольный, а значит сумма острых углов равна 90°, а значит ∠В=90°-60°=30°

2) В треугольнике напротив меньшего угла лежит меньшая сторона. В нашем случае меньший ∠B, а значит меньший катет АС.

3) По мимо этого, т.к. катет АС лежит напротив угла в 30°, то по свойству прямоугольного треугольника он равен половине гипотенузы, т.е. АС=АВ/2

3) По условию АВ-АС=15

АВ-(АВ\2)=15

АВ/2=15

АВ=15*2

АВ=30 см.

ответ: 30 см.

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.