Дан равнобедренный треугольник ABC, АС=ВС. Сторона АВ= 4√6 см, АЕ= 21 см. Найдите ОD, если О – точка пересечения медиан AE и CD.

194

299

Посмотреть ответы 2

Ответы на вопрос:

pallnash

Геометрия

4,6(48 оценок)

Примем половину боковой стороны за х, вся сторона равна 2х.

Косинус угла В при основании равен (4√6/2)/2х = √6/х.

Косинус этого же угла определим по теореме косинусов из треугольника АВЕ: cos B = (4√6)² + x² - 21²)/(2*(4√6)*x.

Приравняем значения косинуса:

(4√6)² + x² - 21²)/(2*(4√6)*x = √6/х.

Приведём к общему знаменателю.

96 + x² - 441 = √6*8√6.

x² = 48 + 441 - 96 = 393.

Отсюда х = √393, а боковая сторона равна 2√393 см.

Найдём высоту СД (она же и медиана к основанию).

СД = √((2√393)² - (2√6)²) = √(1572 - 24) = √1548 = 6√43 ≈ 39,34463 см.

По свойству медиан ОД = (1/3)СД = 2√43 ≈ 13,11488.

ответ: ОД = 2√43 см.

ersultanplay

Геометрия

4,7(86 оценок)

Объяснение:

Мало данных. Неизвестно, в какой четверти лежит угол.

a) Если это I четверть, т.е.

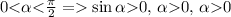
$0 {} 0 ,\,\tg \alpha {}0,\,\ctg \alpha {}0\\$

$cos\alpha = \frac{5}{13} \: \: m.k. \: \: { sin}^{2} \alpha + cos^{2} \alpha = 1 \\ = sin \: \alpha = \sqrt{1 - cos^{2} \alpha } \\ sin \: \alpha = \sqrt{1 - {( \tfrac{5}{13})}^{2} } = \sqrt{1 - \tfrac{25}{169} } = \\ = \sqrt{ \frac{169 - 25}{169} } = \sqrt{ \frac{144}{169} } = \frac{12}{13} \\ \\ tg \: \alpha = \frac{ \sin \alpha }{ \cos \alpha } = \frac{12}{13}{: } \frac{5}{13} = \frac{12}{13} {\times} \frac{13}{5} = \\ = \frac{12}{5} = 2.4 \\ ctg \: \alpha = \frac{ \cos \alpha }{ \sin \alpha } = \frac{1}{tg \: \alpha } = \frac{5}{12} \\$

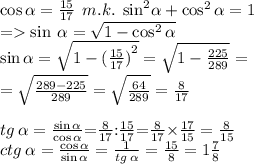
$\cos\alpha = \frac{15}{17} \: \: m.k. \: \: { \sin}^{2} \alpha + \cos^{2} \alpha = 1 \\ = \sin \: \alpha = \sqrt{1 - \cos^{2} \alpha } \\ \sin \alpha = \sqrt{1 - {( \tfrac{15}{17})}^{2} } = \sqrt{1 - \tfrac{225}{289} } = \\ = \sqrt{ \frac{289 - 225}{289} } = \sqrt{ \frac{64}{289} } = \frac{8}{17} \\ \\ \small tg \: \alpha = \frac{ \sin \alpha }{ \cos \alpha }{ =} \frac{8}{17}{: } \frac{15}{17} {=} \frac{8}{17} {\times} \frac{17}{15} = \frac{8}{15} \\ \small \: ctg \: \alpha = \frac{ \cos \alpha }{ \sin \alpha } = \frac{1}{tg \: \alpha } = \frac{15}{8} = 1 \frac{7}{8} \\$

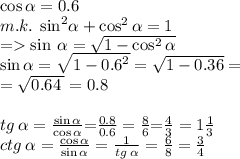
$\cos\alpha =0.6 \\ m.k. \: \: { \sin}^{2} \alpha + \cos^{2} \alpha = 1 \\ = \sin \: \alpha = \sqrt{1 - \cos^{2} \alpha } \\ \sin \alpha = \sqrt{1 - {0.6}^{2} } = \sqrt{1 - 0.36 } = \\ = \sqrt{ 0.64 \: } = 0.8 \\ \\ \small tg \: \alpha = \frac{ \sin \alpha }{ \cos \alpha }{ =} \frac{0.8}{0.6} = \frac{8}{6} {=} \frac{4}{3} = 1 \frac{1}{3} \\ \small \: ctg \: \alpha = \frac{ \cos \alpha }{ \sin \alpha } = \frac{1}{tg \: \alpha } = \frac{6}{8} = \frac{3}{4} \\$

(Если это 4 четверть т.е. 3П/2 < а < 2П,

тогда sin a < 0, tg a < 0, ctg a < 0

и при вычислении sin a перед знаком корня должен стоять знак минуса)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.