Математика: Найти предел функций двух переменных 88 и 91

kolya1pokachalov

14.02.2022 15:50

Математика

Есть ответ 👍

Найти предел функций двух переменных 88 и 91

291

368

Посмотреть ответы 2

Ответы на вопрос:

tanya665444

Математика

4,8(44 оценок)

88) e; 91) 0

Пошаговое объяснение:

88) Перейдем к полярным координатам:

$\lim\limits_{x\to 0,y\to 0} (1+x^2+y^2)^{\frac{1}{x^2+y^2}}=\left[x=r\cos\varphi, y=r\sin\varphi\right]=\lim\limits_{r\to 0} (1+r^2)^{\frac{1}{r^2}}=e$

91) Для достаточно больших значений y [на самом деле, можно явно указать, что |y|≥1, но такая конкретика здесь не важна] верно 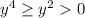$y^4\geq y^20$ .

Тогда 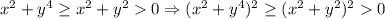$x^2+y^4\geq x^2+y^20\Rightarrow (x^2+y^4)^2\geq (x^2+y^2)^20$ , откуда, с учетом неравенства о средних,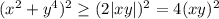 $(x^2+y^4)^2\geq (2|xy|)^2=4(xy)^2$

Но тогда

$\dfrac{(x+y)^2}{(x^2+y^4)^2}\leq \dfrac{(x+y)^2}{4(xy)^2}=\underbrace{\dfrac{1}{4}\left(\dfrac{1}{y}+\dfrac{1}{x}\right)^2}_{g(x)}$

Очевидно, 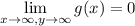$\lim\limits _{x\to\infty,y\to\infty}g(x)=0$ . При этом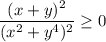 $\dfrac{(x+y)^2}{(x^2+y^4)^2}\geq 0$

Значит,

$0\leq \lim\limits _{x\to\infty,y\to\infty}\dfrac{(x+y)^2}{(x^2+y^4)^2}\leq 0\Rightarrow \lim\limits _{x\to\infty,y\to\infty}\dfrac{(x+y)^2}{(x^2+y^4)^2}=0$

елена13333

Математика

4,7(11 оценок)

Ймовірність того, що студент знає відповідь на вирадково вибране запитання: 25/30

Ймовірність того, що не знає: 5/30

Ймовірність того,що студент знає відповідь на 2 запитання із 3:

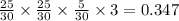
$\frac{25}{30} \times \frac{25}{30} \times \frac{5}{30} \times 3 = 0.347$

До речі, цікаво, що ймовірність того, що студент знає відповідь на 3 запитання із 3 буде 58%

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.