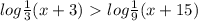Ответы на вопрос:
Задание. Найдите наибольшее целое решение неравенства: 
Решение. Выпишем ограничения логарифмов:
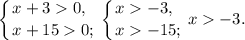
По свойству логарифма 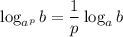 имеем:
имеем:
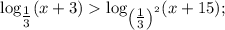
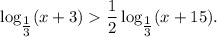
По свойству логарифма 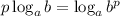 имеем:
имеем:
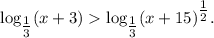
По свойству степеней ![a^{\tfrac{m}{n} } = \sqrt[n]{a^{m}}](/tpl/images/4514/7512/f52d1.png) имеем:
имеем:

Поскольку основание логарифма 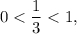 при переходе к подлогарифмическим выражениям знак неравенства должен изменится на противоположный:
при переходе к подлогарифмическим выражениям знак неравенства должен изменится на противоположный:
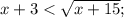

Неравенство вида 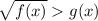 равносильно
равносильно 
Имеем:
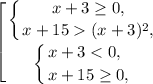
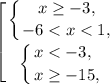
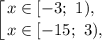
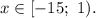
Учитывая ограничения 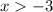 получаем решение:
получаем решение: 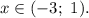
Наибольшим целым решением данного неравенства является число 0.
ответ: 0.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
АААА! 35 баллов тому, кто решит и подробно опишет решение! На стеллаже библиотеки...
 Катеринка22884111.04.2022 10:04
Катеринка22884111.04.2022 10:04 -
Найдите углы выпуклого семиугольника, если два из них равны по 170 °, а остальные...
 pakapika11.02.2022 02:27
pakapika11.02.2022 02:27 -
А)какой наименьший радиус (в единичных отрезках) должен быть у озера чтобы все...
 samyi116umni01.06.2022 04:12
samyi116umni01.06.2022 04:12 -
В каких точках касательная к графику функции у=корень из выражения (2х-1) образует...
 BorzikovaLiza528.06.2020 19:51
BorzikovaLiza528.06.2020 19:51 -
Опишите функции у – х2 и у = х3 (область определения, четность-нечетность, критические...
 nastyskabaterfp08pfs22.08.2022 18:53
nastyskabaterfp08pfs22.08.2022 18:53 -
Ребра прямоугольного параллелепипеда 12 см, 6см, 4см. Найти радиус описанного шара....
 klokova049otccwt23.07.2020 01:11
klokova049otccwt23.07.2020 01:11 -
Три літаки здійснюють регулярні рейси з Одеси. Один з них повертається через 4...
 maxim19943106.06.2020 11:41
maxim19943106.06.2020 11:41 -
1. Исследовать свойства и построить график функции y=x^3-6x^2+5x...
 hohotuchka05.12.2021 22:53
hohotuchka05.12.2021 22:53 -
Дифференциальное уравнение Дифференциальное уравнение...
 ikasatkina200829.06.2023 01:32
ikasatkina200829.06.2023 01:32 -
Диаметр окружности равен 8,61 см. Значение числа π≈3,14. Определи длину C этой...
 лол163427.06.2023 04:16
лол163427.06.2023 04:16

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.