Математика: Объясните, как найти точку x₀ и производную в точке x₀

mlpfim2004

18.03.2020 08:29

Математика

Есть ответ 👍

Объясните, как найти точку x₀ и производную в точке x₀

172

183

Посмотреть ответы 3

Ответы на вопрос:

Елена21st

Математика

4,6(32 оценок)

1) f'(x₀)=-2

2)x₀=-1/2

Пошаговое объяснение:

f'(x₀)=-2 (коэффициент при x в уравнении прямой)

f'(x)=2*4x³-1=8x³-1

8x³-1=-2

8x³=-1

x₀=-1/2

ilyapleshakov29

Математика

4,7(55 оценок)

f'(x₀) = -2

x₀ = -0.5

Пошаговое объяснение:

у= kx+b

у нас есть уравнение прямой, которой должна быть параллельна касательная. значит у нас есть коэффициент к при х для касательной

у = -2 *х +7

а этот коэффициент еще и значение производной функции в точке х₀

f'(x₀) = -2

значит, найдем производную и приравняем ее к -2, т.е f'(x₀)= -2

(2x⁴ -x+1)' = 8x³ -1

8x₀³ -1 = -2 8x₀³ = -1

$\displaystyle x_0=\sqrt[3]{-\frac{1}{8} } =\pm \frac{1}{2} =\pm 0.5$

таким образом мы получили две возможных точки,

проверим их

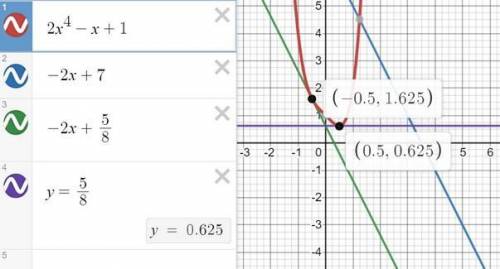
точка x₀= 0,5 f'(0.5) = 8*(0.5)³-1 = 0 в этой точке касательная не параллельна заданной прямой (более того, она параллельна оси ох, тк. коэффициент при х к=0)

точка x₀= 0,5 f'(0.5) = 8*(-0.5)³-1 = -2 в этой точке касательная параллельна заданной прямой

ответ

f'(x₀) = -2

x₀ = -0.5

Объясните, как найти точку x₀ и производную в точке x₀

murad2097

Математика

4,5(55 оценок)

ответ:

пошаговое объяснение:

5 1/6m - 2 1/4m + 1 1/3m=m * (5 1/6-2 1/4+1 1/3)=8/51 * (5 2/12 - 2 3/12 + 1 4/12) = 8/51 * (4 14/12 - 2 3/12 + 1 4/12)= 8/51 * 4 3/12 = 8/51 * 4 1/4 = 8²/51³ * 17/4=2/3

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.