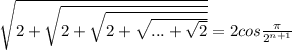Алгебра: Докажите равенство Все это равенство n радикалов

rhenfzj

03.11.2021 14:08

Алгебра

Есть ответ 👍

Докажите равенство $\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{...+\sqrt{2} } } } } =2cos\frac{\pi }{2^{n+1} }$
Все это равенство n радикалов

214

458

Посмотреть ответы 2

Ответы на вопрос:

единорог106

Алгебра

4,6(100 оценок)

Объяснение:

Формула:

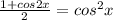
$\frac{1+cos2x}{2} =cos^{2}x$

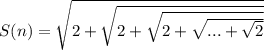
$S(n)=\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{...+\sqrt{2} } } } }$

S(n) - n радикалов

Используем метод мат индукции

1) Покажем верность равенства при n=1, 2, 3

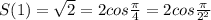
$S(1)=\sqrt{2}=2cos\frac{\pi }{4}=2cos\frac{\pi }{2^{2} }$

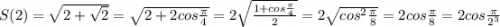
$S(2)=\sqrt{2+\sqrt{2} }=\sqrt{2+2cos\frac{\pi }{4} }=2\sqrt{\frac{1+cos\frac{\pi }{4}}{2} } =2\sqrt{cos^{2}\frac{\pi }{8} } =2cos\frac{\pi }{8}=2cos\frac{\pi }{2^{3} }$

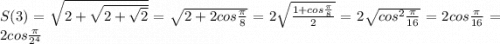
$S(3)=\sqrt{2+\sqrt{2+\sqrt{2} } }=\sqrt{2+2cos\frac{\pi }{8} }=2\sqrt{\frac{1+cos\frac{\pi }{8}}{2} } =2\sqrt{cos^{2}\frac{\pi }{16} } =2cos\frac{\pi }{16}=2cos\frac{\pi }{2^{4} }$

2) Предположим, что равенство верно при n=k

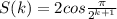
$S(k)=2cos\frac{\pi }{2^{k+1} }$

3) Покажем, , что равенство верно при n=k+1

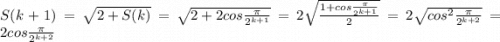
$S(k+1)=\sqrt{2+S(k) }=\sqrt{2+2cos\frac{\pi }{2^{k+1} } }=2\sqrt{\frac{1+cos\frac{\pi }{2^{k+1} }}{2} } =2\sqrt{cos^{2}\frac{\pi }{2^{k+2} } } =2cos\frac{\pi }{2^{k+2}}$

Ч.т.д.

vitaliygrg

Алгебра

4,6(1 оценок)

100%-20%=80 чтобы найти процент от числа,нужно оба эти числа разделить на 10, а потом перемножить 180*8=1440 рублей - заплатит со скидкой на рубашку 100%-30%=70 360*7=2520 рублей - заплатит за туфли со скидкой 100%-40%=60 100*6=600 рублей - заплатит за запонки со скидкой самая дешевая покупка это рубашка и туфли со скидкой, а запонки без скидки 1400+2520+1000=4920 рублей - обойдется вся покупка ответ: 4920

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.