Задача с конусом!! Вычислить наибольший объём конуса, если длина образующей равна 43,8 см: V = [пропуск] * √[пропуск] π см³

257

416

Посмотреть ответы 2

Ответы на вопрос:

ksktys

Геометрия

4,4(52 оценок)

V = 6224,272 * √3 π см³

Объяснение:

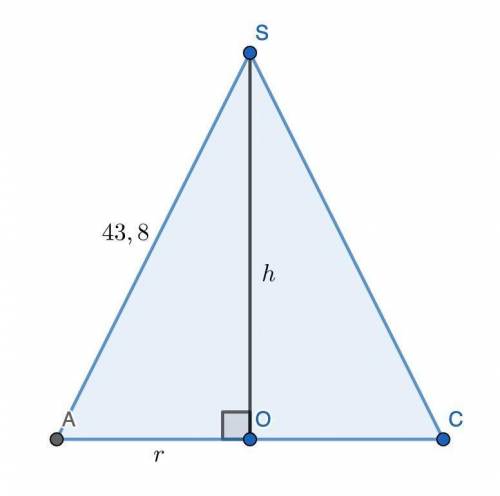
Рассмотрим осевое сечение конуса (см. рис.). SO — высота конуса (h), AO — радиус (r), AS — образующая конуса (43,8 см). Тогда по теореме Пифагора r² + h² = 43,8².

Объём конуса вычисляется по формуле 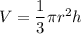$V=\dfrac{1}{3}\pi r^2h$ . Из предыдущего уравнения r² = 43,8² - h². Подставим это в уравнение объёма:

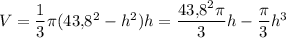
$V=\dfrac{1}{3}\pi (43{,}8^2-h^2)h=\dfrac{43{,}8^2\pi}{3}h-\dfrac{\pi}{3}h^3$

Найдём максимальное значение с производной:

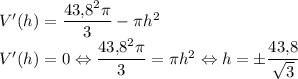
$V'(h)=\dfrac{43{,}8^2\pi}{3}-\pi h^2\\V'(h)=0\Leftrightarrow \dfrac{43{,}8^2\pi}{3}=\pi h^2\Leftrightarrow h=\pm\dfrac{43{,}8}{\sqrt{3}}$

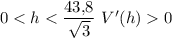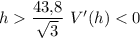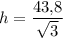Будем рассматривать только положительные значения h, так как отрицательной высота быть не может. При , при $h\dfrac{43{,}8}{\sqrt{3}}\ V'(h)$ . Значит, $h=\dfrac{43{,}8}{\sqrt{3}}$ — точка максимума. При данном значении h объём конуса максимален.

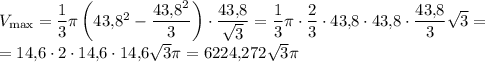
$V_{\max}=\dfrac{1}{3}\pi\left(43{,}8^2-\dfrac{43{,}8^2}{3}\right)\cdot\dfrac{43{,}8}{\sqrt{3}}=\dfrac{1}{3}\pi \cdot\dfrac{2}{3}\cdot 43{,}8\cdot 43{,}8\cdot\dfrac{43{,}8}{3}\sqrt{3}=\\=14{,}6\cdot 2\cdot 14{,}6\cdot 14{,}6\sqrt{3}\pi=6224{,}272\sqrt{3}\pi$

Задача с конусом!! Вычислить наибольший объём конуса, если длина образующей равна 43,8 см: V = [проп

dtgyhyccubbycy

Геометрия

4,7(13 оценок)

ответ:

45 см²

объяснение:

s=0,5·(18+12)·3=45

высота трапеции равна 3 см

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.