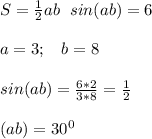fggyhuhgyg

25.07.2021 19:13

Геометрия

Есть ответ 👍

Площадь треугольника равна 6.Найдите угол между сторонам длиной 3 и 8

180

347

Посмотреть ответы 3

Ответы на вопрос:

Gabueva02

Геометрия

4,4(68 оценок)

∠(ab)=30°

Объяснение:

$S=\frac{1}{2} ab\;\ sin(ab)=6a=3;\;\;\ b=8sin(ab)=\frac{6*2}{3*8} =\frac{1}{2} (ab)=30^0$

∠(ab)=30°

kate050804

Геометрия

4,7(54 оценок)

30°

Объяснение:

В данном случае нам очень знание всех формул на площадь. А именно через синус. Формула имеет вид

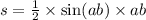
$s = \frac{1}{2} \times \sin(ab) \times ab \\$

Где ab - угол между смежными сторонами и a и b длина этих сторон.

Зная синус угла между сторонами, мы найдем угол между сторонами по арксинусу.

Выразим синус

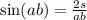
$\sin(ab) = \frac{2s}{ab}$

Подставим значения и получим 0.5

Если это была бы тригонометрия, то угол равнялся

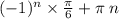
$( - 1)^n \times \frac{\pi}{6} + \pi \: n$

Где n - целое число.

Но в геометрии углы не могут быть отрицательными или больше 180°. Поэтому рассмотрим 2 варианта: 30° и 150°. Надо думать логически: напротив угла стоит сторона либо самая большая, либо самая маленькая (не факт, но наверняка). Рассмотрим случай с большей стороной.

Эта сторона будет больше 8; 9, например (на самом деле больше, но я просто привел пример). Как мы знаем, площадь треугольника равна полупроизведению основания и высоты. Тогда их произведение равно 12. Если наша сторона равна 8, то высота будет равна максимум 1.5. На самом деле, сторона это равна около 11. Попробуем проверить с формулы Герона. Не проходит, тогда правильный ответ 30°.

(Я вырезал часть решения с нахождением третьей стороны по теореме косинусов и подставлению в формулу Герона, но я посчитал, что сделал неправильно, поэтому оставил часть решения на вас, так как мое неоптимально)

nata524

Геометрия

4,7(16 оценок)

извиняй по украински не читаю

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.