Математика: Исследовать ряд на сходимость.

enotkcovi

21.04.2023 09:48

Математика

Есть ответ 👍

Исследовать ряд на сходимость.

141

191

Посмотреть ответы 2

Ответы на вопрос:

sonicbum

Математика

4,8(82 оценок)

ответ: ряд сходится .

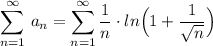
$\displaystyle \sum \limits _{n=1}^{\infty }\, a_{n}=\sum \limits _{n=1}^{\infty }\frac{1}{n}\cdot ln\Big(1+\frac{1}{\sqrt{n}}\Big)$

Подберём ряд сравнения : 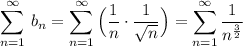$\displaystyle \sum \limits _{n=1}^{\infty }\, b_{n}=\sum \limits _{n=1}^{\infty }\Big(\frac{1}{n}\cdot \frac{1}{\sqrt{n}}\Big)=\sum \limits _{n=1}^{\infty }\frac{1}{n^{\frac{3}{2}}}$ .

Этот ряд является обобщённым гармоническим сходящимся рядом , так как показатель степени 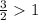$\frac{3}{2}1$ . Применим к рядам предельный признак сравнения .

$\displaystyle \lim\limits_{n \to \infty}\frac{a_{n}}{b_{n}}=\displaystyle \lim\limits_{n \to \infty}\frac{\dfrac{1}{n}\cdot ln\Big(1+\dfrac{1}{\sqrt{n}}\Big)}{\dfrac{1}{n^{\frac{3}{2=\displaystyle \lim\limits_{n \to \infty}\frac{n^{\frac{3}{2}}\cdot ln\Big(1+\dfrac{1}{\sqrt{n}}\Big)}{n}==\Big[\ ln(1+\alpha (x))\sim \alpha (x)\ \ ,\ esli\ \alpha(x)\to 0\ \ ,\ \ \frac{1}{\sqrt{n}}}\to 0\ \ \ pri\ \ n\to \infty \ \Big]=$

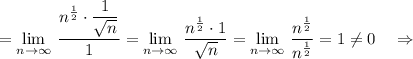
$=\displaystyle \lim\limits_{n \to \infty}\, \frac{n^{\frac{1}{2}}\cdot \dfrac{1}{\sqrt{n}}}{1}=\lim\limits_{n \to \infty}\, \frac{n^{\frac{1}{2}}\cdot 1}{\sqrt{n}}=\lim\limits_{n \to \infty}\, \frac{n^{\frac{1}{2}}}{n^{\frac{1}{2}}}=1\ne 0\ \ \ \Rightarrow$

Ряды ведут себя одинаково, оба сходятся .

nastua89723

Математика

4,5(34 оценок)

1) 80*0,2125=17(отл) 2) 90*0,2= 18(отл) 3) 18-17=1( больше на 1 человека ) ответ : в 6 отличников больше чем в 5 на 1 человека

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.