ABCDA1B1C1D1 - прямоугольный параллелепипед. AB = 3, BC = 4, CC, = 5.
Назовите векторы, равные векторам
AB, BC, CC1,
Назовите длины векторов:
AD, AA1, AD1, AC, BD1

115

344

Посмотреть ответы 1

Ответы на вопрос:

berdyugin

Геометрия

4,8(63 оценок)

ответ: 75 (ед. площади)

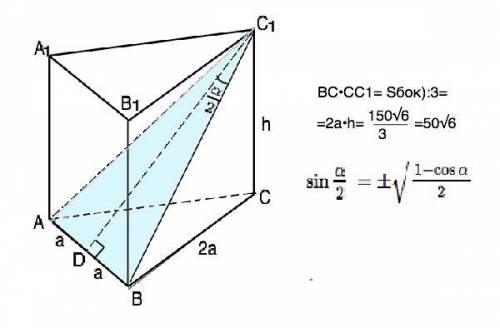
Объяснение: Боковые рёбра правильной призмы перпендикулярны основанию, а в основании лежит правильный многоугольник, ⇒

∆ АВС - правильный.

По одной из формул площади треугольника Ѕ(АС1В)=0,5•АС1•ВС1•sinα

sinα=3/5 (дано).

Диагонали граней правильной призмы равны. ⇒ АС1=ВС1

На рисунке C1D делит угол пополам - С1D биссектриса ( медиана, высота) равнобедренного треугольника АС1В.

AD=BD

ВС1=BD/sin(BC1D)=BD/sin0,5α

Примем сторону основания равной 2а. Тогда BD=a.

По формуле половины угла sin0,5α=√((1-cosα)/2)

cosα=√(1-sin² α)=√(1-9/25)=4/5

sin0,5α=√((1-4/5):2)=√(1/10)=1/√10

BC1=a:1/√10 BC1=a√10

ВВ1С1С-прямоугольник. ВС1 - его диагональ.

Из ∆ ВСС1 по т.Пифагора СС1=√(BC1²-BC²)=√(10a²-4a²)=a√6

Из площади боковой поверхности площадь одной боковой грани BC•CC1=(150√6):3=50√6⇒

2a•a√6=50√6

2a²=50 ⇒ a=√(50/2)=5

АС1=ВС1=5√10

Ѕ(АС1В)=0,5•АС1•ВС1•sin(AC1B)=0,5•(5√10)²•3/5=0,5•250•3/5=75 (ед. площади)

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.