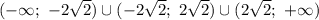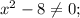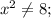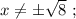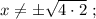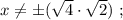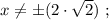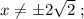Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Сумма двух чисел ровна 40 первая 8, найди второе число...
 yyyoooppp12.02.2023 08:58
yyyoooppp12.02.2023 08:58 -
На какой вопрос отвечает слово гореть...
 niketa77708.03.2020 11:22
niketa77708.03.2020 11:22 -
Подать в выгляди степення: b седьмою степени иbв рретей степени...
 Ученик000520524.09.2020 03:20
Ученик000520524.09.2020 03:20 -
При пересечении двух параллельных прямых секущей образовались односторонние...
 JANAAAAAA09.11.2021 15:55
JANAAAAAA09.11.2021 15:55 -
2x+1+5(x-2)=-4(3-x)+1 сколько получится...
 неточно125.08.2021 04:53
неточно125.08.2021 04:53 -
На рисунке изображен график y=f (x)производной функцииf(x),определенной...
 g11uru01.08.2022 20:48
g11uru01.08.2022 20:48 -
дам оценку 5.0 разложить на множители c² - 9 a² - 4 x² - 16 d²...
 Rona123404.06.2022 06:28
Rona123404.06.2022 06:28 -
Реши уравнение.Вынеси Х за скобки....
 Nikitunnik06.09.2022 16:16
Nikitunnik06.09.2022 16:16 -
При каких значениях параметра а система уравнений имеет три решения....
 zakharizh200129.01.2023 15:59
zakharizh200129.01.2023 15:59 -
Разложите на множители 12a³-4a⁴ ...
 ксззххххх23.03.2020 01:09
ксззххххх23.03.2020 01:09

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.